题目内容
3.已知等差数列{an}的前n项和为Sn=-n2+(10+k)n+(k-1),则实数k=1,an=-2n+12,Sn的最大值为30.分析 由等差数列前n项和的性质可得k-1=0,求得k,代入前n项和后利用二次函数的最值求得Sn的最大值,再由前n项和求得首项和公差,则通项公式可求.
解答 解:∵Sn=-n2+(10+k)n+(k-1)为等差数列的前n项和,∴k-1=0,即k=1;
则Sn=-n2+11n,对称轴方程为n=$\frac{11}{2}$,
∵n∈N*,∴当n=5或6时Sn有最大值为30;
a1=S1=10,a2=S2-S1=18-10=8,
∴d=a2-a1=-2,则an=-2n+12.
故答案为:1,-2n+12,30.
点评 本题考查了等差数列的通项公式,考查了等差数列的前n项和,是基础题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
14.已知 (1-2i)z=5(i为虚数单位),则复数z在复平面内对应的点所在象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
8.已知过双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的中心的直线交双曲线于点A,B,在双曲线C上任取与点A,B不重合的点P,记直线PA,PB,AB的斜率分别为k1,k2,k,若k1k2>k恒成立,则离心率e的取值范围为( )
| A. | 1<e<$\sqrt{2}$ | B. | 1<e≤$\sqrt{2}$ | C. | e>$\sqrt{2}$ | D. | e≥$\sqrt{2}$ |
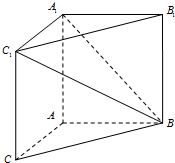 如图,在三棱柱ABC-A1B1C1中,AB=3,AA1=AC=4,AA1⊥平面ABC; AB⊥AC,
如图,在三棱柱ABC-A1B1C1中,AB=3,AA1=AC=4,AA1⊥平面ABC; AB⊥AC, 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴为4,离心率e=$\frac{\sqrt{3}}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴为4,离心率e=$\frac{\sqrt{3}}{2}$.