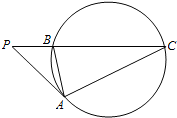
题目内容
19.计算:log2$\frac{\sqrt{2}}{2}$=$-\frac{1}{2}$,2${\;}^{lo{g}_{2}3+lo{g}_{4}3}$=$3\sqrt{3}$.分析 直接利用对数运算法则化简求值即可.
解答 解:log2$\frac{\sqrt{2}}{2}$=log2${2}^{-\frac{1}{2}}$=-$\frac{1}{2}$;
2${\;}^{lo{g}_{2}3+lo{g}_{4}3}$=${2}^{{\;}^{lo{g}_{2}3+\frac{1}{2}lo{g}_{2}3}}$=${2}^{{\;}^{lo{g}_{2}(3•{3}^{\frac{1}{2}})}}$=3$\sqrt{3}$.
故答案为:$-\frac{1}{2}$;$3\sqrt{3}$.
点评 本题考查对数的运算法则的应用,基本知识的考查.

练习册系列答案
相关题目
9.已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,短轴的一个端点为M,直线l:3x-4y=0交椭圆E于A,B两点,若|AF|+|BF|=4,点M到直线l的距离不小于$\frac{4}{5}$,则椭圆E的离心率的取值范围是( )
| A. | (0,$\frac{\sqrt{3}}{2}$] | B. | (0,$\frac{3}{4}$] | C. | [$\frac{\sqrt{3}}{2}$,1) | D. | [$\frac{3}{4}$,1) |
14.设a,b是实数,则“a+b>0”是“ab>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
18.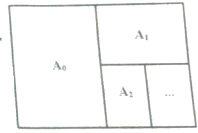 An(n∈N)系列的纸张规格如图,其特点是
An(n∈N)系列的纸张规格如图,其特点是
①A0,A1,A2,…An所有规格的纸张的长宽比都相同;
②A0对裁后可以得到两张A1,A1对裁后可以得到两张A2,…,An-1对裁后可以得到两张An;
若梅平方厘米重量为b克的A0,A1,A2,…An纸张各一张,其中A4纸较短边的长为a厘米,记这(n+1)纸张的重量之和为Sn+1,则下列论断错误的是( )
 An(n∈N)系列的纸张规格如图,其特点是
An(n∈N)系列的纸张规格如图,其特点是①A0,A1,A2,…An所有规格的纸张的长宽比都相同;
②A0对裁后可以得到两张A1,A1对裁后可以得到两张A2,…,An-1对裁后可以得到两张An;
若梅平方厘米重量为b克的A0,A1,A2,…An纸张各一张,其中A4纸较短边的长为a厘米,记这(n+1)纸张的重量之和为Sn+1,则下列论断错误的是( )
| A. | 存在n∈N,使得Sn+1=32$\sqrt{2}$a2b | B. | 存在n∈N,使得Sn+1=16$\sqrt{2}$a2b | ||
| C. | 对于任意n∈N,使得Sn+1≤32$\sqrt{2}$a2b | D. | 对于任意n∈N,使得Sn+1≥16$\sqrt{2}$a2b |
19. 某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大的为( )
某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大的为( )
 某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大的为( )
某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大的为( )| A. | 2$\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{6}$ |