题目内容
4.已知实数x,y满足x2+y2≤1,则|2x+y-4|+|6-x-3y|的最大值是15.分析 由题意可得2x+y-4<0,6-x-3y>0,去绝对值后得到目标函数z=-3x-4y+10,然后结合圆心到直线的距离求得|2x+y-4|+|6-x-3y|的最大值.
解答 解:如图,
由x2+y2≤1,
可得2x+y-4<0,6-x-3y>0,
则|2x+y-4|+|6-x-3y|=-2x-y+4+6-x-3y=-3x-4y+10,
令z=-3x-4y+10,得$y=-\frac{3}{4}x-\frac{z}{4}+\frac{5}{2}$,
如图,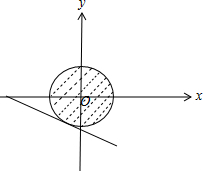
要使z=-3x-4y+10最大,则直线$y=-\frac{3}{4}x-\frac{z}{4}+\frac{5}{2}$在y轴上的截距最小,
由z=-3x-4y+10,得3x+4y+z-10=0.
则$\frac{|z-10|}{5}=1$,即z=15或z=5.
由题意可得z的最大值为15.
故答案为:15.
点评 本题考查了简单的线性规划,考查了数形结合的解题思想方法,考查了数学转化思想方法,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.若a,b∈(0,2),则函数f(x)=$\frac{1}{3}$ax3+2x2+4bx+1存在极值的概率为( )
| A. | $\frac{1+2ln2}{4}$ | B. | $\frac{3-2ln2}{4}$ | C. | $\frac{1+ln2}{2}$ | D. | $\frac{1-ln2}{2}$ |