某四面体的三视图如图所示.正视图.俯视图都是腰长为2的等腰直角三角形.侧视图是边长为2的正方形.则此四面体的四个面中面积最大的为( )A．2$\sqrt{2}$B．4C．2$\sqrt{3}$D．2$\sqrt{6}$ 题目和参考答案——青夏教育精英家教网—

题目内容

19．

某四面体的三视图如图所示，正视图、俯视图都是腰长为2的等腰直角三角形，侧视图是边长为2的正方形，则此四面体的四个面中面积最大的为（　　）

A．

2$\sqrt{2}$

B．

C．

2$\sqrt{3}$

D．

2$\sqrt{6}$

分析由三视图知该几何体为棱锥，其中SC⊥平面ABCD；四面体S-ABD的四个面中SBD面的面积最大，三角形SBD是边长为2$\sqrt{2}$的等边三角形，即可求出四面体的四个面中面积最大的面积．

解答解：由三视图知该几何体为棱锥S-ABD，其中SC⊥平面ABCD；四面体S-ABD的四个面中SBD面的面积最大，三角形SBD是边长为2$\sqrt{2}$的等边三角形，

所以此四面体的四个面中面积最大的为$\frac{\sqrt{3}}{4}×8$=2$\sqrt{3}$．
故选：C．

点评本题考查三视图，考查面积的计算，确定三视图对应直观图的形状是关键．

练习册系列答案

10．设x，y∈R，满足$\left\{\begin{array}{l}{（x-1）^{5}+2x+sin（x-1）=3}\\{（y-1）^{5}+2y+sin（y-1）=1}\end{array}\right.$，则x+y=（　　）

7．已知甲，乙两名运动员的罚球命中率分别为0.8和0.6，甲在无人防守下上篮命中率为0.95，已知罚球中一球得1分，上篮命中得2分．
（1）若两人各罚两次球，求一共罚中2次的概率；
（2）假若在一场比赛中甲获得一次无人防守的上篮机会，此时防守球员无法形成有效防守，只能选择犯规或什么都不做，假设防守球员犯规，甲球员仍然有$\frac{1}{5}$的概率命中此球，若命中得到2分并追加一次罚球，若在防守球员犯规的情况下甲没有命中，则甲罚球两次，问此时防守球员应不应该犯规？

14．设方程log₂x-（$\frac{1}{2}$）^x=0与log${\;}_{\frac{1}{4}}$x-（$\frac{1}{4}$）^x=0的根分别为x₁，x₂，则（　　）

0＜x₁x₂＜1

x₁x₂=1

1＜x₁x₂＜2

x₁x₂≥2

4．若a，b∈（0，2），则函数f（x）=$\frac{1}{3}$ax³+2x²+4bx+1存在极值的概率为（　　）

11．已知平面α∥平面β，异面直线a，b分别在α，β内，直线l⊥a，l⊥b，求证：l⊥α，l⊥β．

8．设f′（x）为函数f（x）的导函数，已知x²f′（x）+xf（x）=lnx，f（e）=$\frac{1}{e}$，则下列结论正确的是（　　）

	A．	f（x）在（0，+∞）单调递增		B．	f（x）在（0，+∞）单调递减
	C．	f（x）在（0，+∞）上有极大值		D．	f（x）在（0，+∞）上有极小值

6．

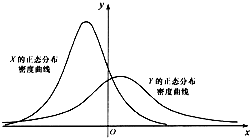设X～N（μ₁，σ₁²），Y～N（μ₂，σ₂²），这两个正态分布密度曲线如图所示．下列结论中正确的是（　　）

	A．	P（Y≥μ₂）≥P（Y≥μ₁）		B．	P（X≤σ₂）≤P（X≤σ₁）
	C．	对任意正数t，P（X≤t）≥P（Y≤t）		D．	对任意正数t，P（X≥t）≥P（Y≥t）

试题分类