题目内容
若对任意的x∈D,均有f1(x)≤f(x)≤f2(x)成立,则称函数f(x)为函数f1(x)到函数f2(x)在区间D上的“折中函数”.已知函数f(x)=(k-1)x-1,g(x)=0,h(x)=(x+1)ln x,且f(x)是g(x)到h(x)在区间[1,2e]上的“折中函数”,则实数k的取值范围为________.
{2}
法一:依题意可知当x∈[1,2e]时,恒有0≤(k-1)x-1≤(x+1)ln x成立.
当x∈[1,2e]时,由(k-1)x-1≥0恒成立,可知k≥1+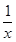 恒成立,又x∈[1,2e]时,
恒成立,又x∈[1,2e]时,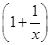 max=2,此时x=1,从而k≥2.
max=2,此时x=1,从而k≥2.
当x∈[1,2e]时,由(k-1)x-1≤(x+1)ln x恒成立,可知k≤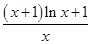 +1恒成立,记
+1恒成立,记
m(x)=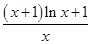 =
=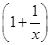 ln x+
ln x+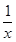 ,
,
其中x∈[1,2e].从而m′(x)=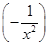 ln x+
ln x+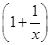
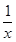 -
-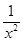 =
=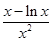 ,易知当x∈[1,2e]时,x>ln x(可以建立函数再次利用导数证明,)所以当x∈[1,2e]时,m′(x)>0,所以m(x)在x∈[1,2e]上是单调递增函数,所以k≤m(x)min+1=m(1)+1=2.
,易知当x∈[1,2e]时,x>ln x(可以建立函数再次利用导数证明,)所以当x∈[1,2e]时,m′(x)>0,所以m(x)在x∈[1,2e]上是单调递增函数,所以k≤m(x)min+1=m(1)+1=2.
综上所述可知k=2,所以实数k的取值范围为{2}.
法2:由于本题的特殊性,可看出g(1)=0,h(1)=0,由题知g(1)≤f(1)≤h(1),显然f(1)=0,即k=2.h′(x)=1+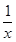 +ln x.在[1,2e]上,h′(x)>1=f′(x),故k=2.
+ln x.在[1,2e]上,h′(x)>1=f′(x),故k=2.
当x∈[1,2e]时,由(k-1)x-1≥0恒成立,可知k≥1+
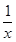 恒成立,又x∈[1,2e]时,
恒成立,又x∈[1,2e]时,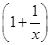 max=2,此时x=1,从而k≥2.
max=2,此时x=1,从而k≥2.当x∈[1,2e]时,由(k-1)x-1≤(x+1)ln x恒成立,可知k≤
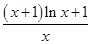 +1恒成立,记
+1恒成立,记m(x)=
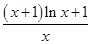 =
=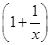 ln x+
ln x+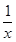 ,
,其中x∈[1,2e].从而m′(x)=
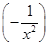 ln x+
ln x+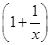
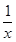 -
-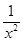 =
=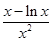 ,易知当x∈[1,2e]时,x>ln x(可以建立函数再次利用导数证明,)所以当x∈[1,2e]时,m′(x)>0,所以m(x)在x∈[1,2e]上是单调递增函数,所以k≤m(x)min+1=m(1)+1=2.
,易知当x∈[1,2e]时,x>ln x(可以建立函数再次利用导数证明,)所以当x∈[1,2e]时,m′(x)>0,所以m(x)在x∈[1,2e]上是单调递增函数,所以k≤m(x)min+1=m(1)+1=2.综上所述可知k=2,所以实数k的取值范围为{2}.
法2:由于本题的特殊性,可看出g(1)=0,h(1)=0,由题知g(1)≤f(1)≤h(1),显然f(1)=0,即k=2.h′(x)=1+
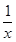 +ln x.在[1,2e]上,h′(x)>1=f′(x),故k=2.
+ln x.在[1,2e]上,h′(x)>1=f′(x),故k=2.
练习册系列答案
相关题目
 是偶函数,
是偶函数, 是它的导函数,当
是它的导函数,当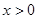 时,
时,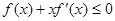 恒成立,且
恒成立,且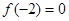 ,则不等式
,则不等式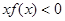 的解集为 。
的解集为 。 ,且对任意实数x,总有
,且对任意实数x,总有 /(x)<3
/(x)<3 <3x-15的解集为( )
<3x-15的解集为( ) x2+4x-3ln x在[t,t+1]上不单调,则t的取值范围是________.
x2+4x-3ln x在[t,t+1]上不单调,则t的取值范围是________.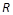 上可导的函数
上可导的函数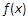 的图形如图所示,
的图形如图所示,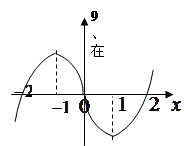 则关于
则关于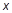 的不等式
的不等式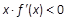 的解集为( ).
的解集为( ).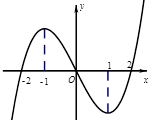




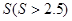 平方米的矩形场地的围墙,要求在前面墙的正中间留一个宽度为2米的出入口,后面墙长度不超过20米,已知后面墙的造价为每米45元,其它墙的造价为每米180元,设后面墙长度为x米,修建此矩形场地围墙的总费用为
平方米的矩形场地的围墙,要求在前面墙的正中间留一个宽度为2米的出入口,后面墙长度不超过20米,已知后面墙的造价为每米45元,其它墙的造价为每米180元,设后面墙长度为x米,修建此矩形场地围墙的总费用为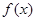 元.
元.
 在
在 上的最大值和最小值分别记为
上的最大值和最小值分别记为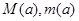 ,求
,求 ;
; 若
若 对
对 恒成立,求
恒成立,求 的取值范围.
的取值范围.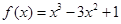 的单调递减区间为( ).
的单调递减区间为( ).