题目内容
已知函数
若 在
在 上的最大值和最小值分别记为
上的最大值和最小值分别记为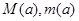 ,求
,求 ;
;
设 若
若 对
对 恒成立,求
恒成立,求 的取值范围.
的取值范围.

若
 在
在 上的最大值和最小值分别记为
上的最大值和最小值分别记为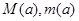 ,求
,求 ;
;设
 若
若 对
对 恒成立,求
恒成立,求 的取值范围.
的取值范围.(1)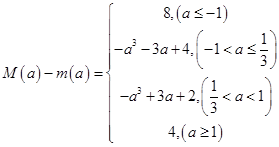 ;(2)
;(2) 的取值范围
的取值范围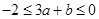 .
.
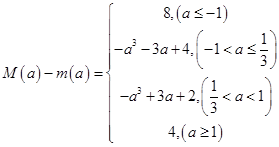 ;(2)
;(2) 的取值范围
的取值范围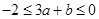 .
.试题分析:(1)若
 在
在 上的最大值和最小值分别记为
上的最大值和最小值分别记为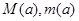 ,求
,求 ,由函数
,由函数 得
得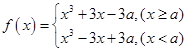 ,求函数在闭区间最值,可用导数法,故求导得
,求函数在闭区间最值,可用导数法,故求导得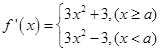 ,由于
,由于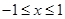 ,故需对
,故需对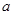 进行讨论,分
进行讨论,分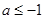 ,
,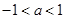 ,
,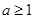 三种情况,利用单调性,分别求出最大值和最小值即可;(2)设
三种情况,利用单调性,分别求出最大值和最小值即可;(2)设 若
若 对
对 恒成立,求
恒成立,求 的取值范围,可令
的取值范围,可令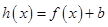 ,由
,由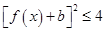 ,得
,得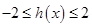 ,即
,即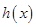 在
在 上的值域是集合
上的值域是集合 的子集,即求
的子集,即求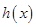 在
在 上的最大值和最小值,让最大值小于等于
上的最大值和最小值,让最大值小于等于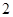 ,最小值大于等于
,最小值大于等于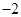 ,即可求出
,即可求出 的取值范围,结合(1)分
的取值范围,结合(1)分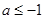 ,
,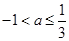 ,
,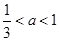 ,
,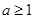 四种情况讨论即可.
四种情况讨论即可.(1)因为
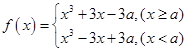 ,所以
,所以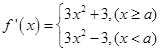 ,由于
,由于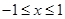 ,
,(ⅰ)当
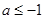 时,有
时,有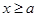 ,故
,故 ,此时
,此时 在
在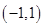 上是增函数,因此
上是增函数,因此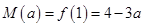 ,
,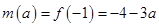 ,
,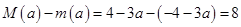
(ⅱ)当
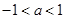 时,若
时,若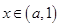 ,
, ,在
,在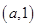 上是增函数,,若
上是增函数,,若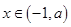 ,
,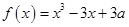 ,在
,在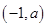 上是减函数,所以
上是减函数,所以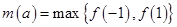 ,
,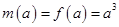 ,由于
,由于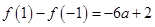 ,因此,当
,因此,当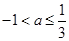 时,
时,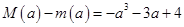 ,当
,当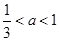 时,
时,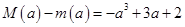 ,
,(ⅲ)当
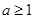 时,有
时,有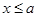 ,故
,故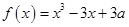 ,此时
,此时 在
在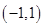 上是减函数,因此
上是减函数,因此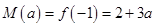 ,
,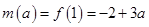 ,故
,故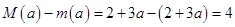 ,综上
,综上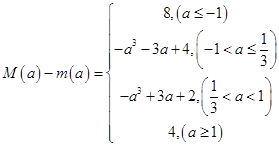 ;
;(2)令
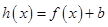 ,则
,则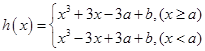 ,
,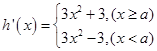 ,因为
,因为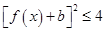 ,对
,对 恒成立,即
恒成立,即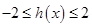 对
对 恒成立,所以由(I)知,
恒成立,所以由(I)知,(ⅰ)当
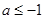 时,
时,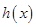 在
在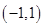 上是增函数,
上是增函数,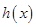 在
在 上的最大值是
上的最大值是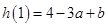 ,最小值是
,最小值是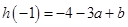 ,则
,则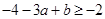 ,且
,且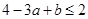 ,矛盾;
,矛盾;(ⅱ)当
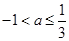 时,
时,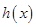 在
在 上的最大值是
上的最大值是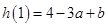 ,最小值是
,最小值是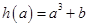 ,所以
,所以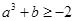 ,
,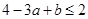 ,从而
,从而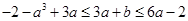 且
且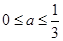 ,令
,令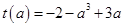 ,则
,则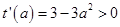 ,
,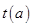 在
在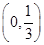 上是增函数,故
上是增函数,故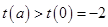 ,因此
,因此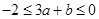 ,
,(ⅲ)当
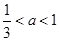 时,
时,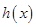 在
在 上的最大值是
上的最大值是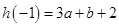 ,最小值是
,最小值是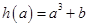 ,所以
,所以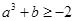 ,
,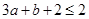 ,解得
,解得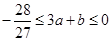 ,
,(ⅳ)当
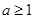 时,
时,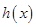 在
在 上的最大值是
上的最大值是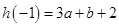 ,最小值是
,最小值是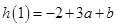 ,所以
,所以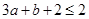 ,
,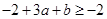 ,解得
,解得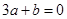 ,综上
,综上 的取值范围
的取值范围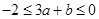 .
.点评:本题主要考查函数最大(最小)值的概念,利用导数研究函数的单调性等基础知识,同时考查推理论证,分类讨论,分析问题和解决问题的综合解题能力.

练习册系列答案
相关题目
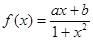 是定义在
是定义在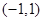 上的奇函数,且
上的奇函数,且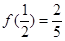 .
.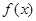 的解析式;
的解析式;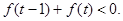 .
.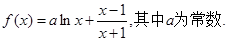
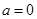 ,求曲线
,求曲线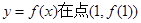 处的切线方程;
处的切线方程; 的单调性.
的单调性. ,若
,若 在
在 上的最小值记为
上的最小值记为 .
. 时,恒有
时,恒有 .
.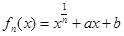
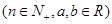 .
.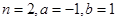 时,求函数
时,求函数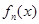 的极值;
的极值;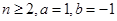 ,证明:
,证明: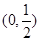 内存在唯一的零点;
内存在唯一的零点;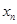 是
是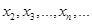 的增减性.
的增减性. .
. 时,讨论
时,讨论 的单调性;
的单调性; ,当
,当 若对任意
若对任意 存在
存在 使
使 求实数
求实数 的取值范围。
的取值范围。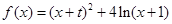 的图象在点
的图象在点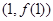 处的切线垂直于
处的切线垂直于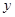 轴.
轴.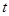 的值;
的值;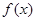 的极值.
的极值. 为定义在(0,+∞)上的可导函数,且
为定义在(0,+∞)上的可导函数,且 恒成立,则不等式
恒成立,则不等式 的解集为______ _____.
的解集为______ _____.