题目内容
若对定义在R上的可导函数f（x），恒有（4-x）f（2x）+2xf′（2x）＞0，（其中f′（2x）表示函数f（x）的导函数f′（x）在2x的值），则f（x）（ ）
| A．恒大于等于0 | B．恒小于0 |
| C．恒大于0 | D．和0的大小关系不确定 |
函数g（x）=
，
则g′(x)=
=
=
=
，
∵（4-x）f（2x）+2xf′（2x）＞0恒成立，
∴当x＞0时，g'（x）＞0，此时函数g（x）单调递增，
当x＜0时，g'（x）＜0，此时函数g（x）单调递减，
∴当x=0时，g（x）取得极小值，同时也是最小值g（0）=0，
∴g（x）=
≥g（0），
即g（x）=
≥0，当x≠0时，g（x）＞0，
∴当x≠0时，f（x）＞0，
∵（4-x）f（2x）+2xf′（2x）＞0恒成立，
∴当x=0时，4f（0）+0＞0恒成立，
∴f（0）＞0，
综上无论x取何值，恒有f（x）＞0，
故选C．
| x4f(2x) |
| ex |
则g′(x)=
| [x4f(2x)]′ex-x4f(2x)?[ex]′ |
| [ex]2 |
| 4x3f(2x)+2x4f′(2x)-x4f(2x) |
| ex |
=
| (4x3-x4)f(2x)+2x4f′(2x) |
| ex |
| x3[(4-x)f(2x)+2f′(2x)] |
| ex |
∵（4-x）f（2x）+2xf′（2x）＞0恒成立，
∴当x＞0时，g'（x）＞0，此时函数g（x）单调递增，
当x＜0时，g'（x）＜0，此时函数g（x）单调递减，
∴当x=0时，g（x）取得极小值，同时也是最小值g（0）=0，
∴g（x）=
| x4f(2x) |
| ex |
即g（x）=
| x4f(2x) |
| ex |
∴当x≠0时，f（x）＞0，
∵（4-x）f（2x）+2xf′（2x）＞0恒成立，
∴当x=0时，4f（0）+0＞0恒成立，
∴f（0）＞0，
综上无论x取何值，恒有f（x）＞0，
故选C．
练习册系列答案
相关题目
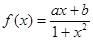是定义在
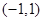上的奇函数，且
.
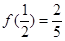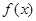的解析式；
.
，
，
.
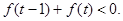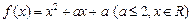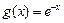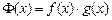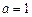时，求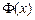
的单调区间；
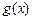在点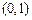
处的切线与直线
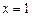及曲线
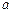，使