题目内容
如图:底面直径为2的圆柱被与底面成 二面角的平面所截,截面是一个椭圆, 则此椭圆的焦距为 .
二面角的平面所截,截面是一个椭圆, 则此椭圆的焦距为 .
 二面角的平面所截,截面是一个椭圆, 则此椭圆的焦距为 .
二面角的平面所截,截面是一个椭圆, 则此椭圆的焦距为 .
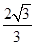
解:由题意可知椭圆的短轴长是220
∵底面直径为2的圆柱被与底面成60°二面角的平面所截,截面是一个椭圆,
∴过椭圆长轴的轴截面图形如图,
∠KJL=30°,JK是底面直径长度为2
由此三角形是直角三角形,故LJ=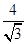
∴椭圆的长轴长为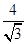 ,短轴长为2
,短轴长为2
即a=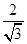 ,b=1,所以c2= a2-b2 =
,b=1,所以c2= a2-b2 = 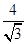 -12 =
-12 =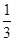 则此椭圆的焦距为
则此椭圆的焦距为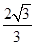
∵底面直径为2的圆柱被与底面成60°二面角的平面所截,截面是一个椭圆,
∴过椭圆长轴的轴截面图形如图,
∠KJL=30°,JK是底面直径长度为2
由此三角形是直角三角形,故LJ=
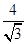
∴椭圆的长轴长为
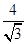 ,短轴长为2
,短轴长为2即a=
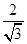 ,b=1,所以c2= a2-b2 =
,b=1,所以c2= a2-b2 = 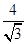 -12 =
-12 =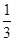 则此椭圆的焦距为
则此椭圆的焦距为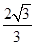

练习册系列答案
相关题目
 的正方体
的正方体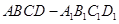 中,
中,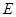 是线段
是线段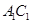 的中点,
的中点, .
.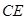 ^
^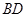 ;
;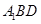 ;
;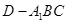 的表面积.
的表面积.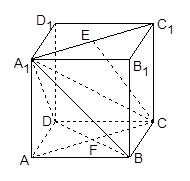
 ,那么该三棱柱的体积为
,那么该三棱柱的体积为
 ,则三棱锥的体积与其外接球体积之比是 。
,则三棱锥的体积与其外接球体积之比是 。 ,则此四面体的棱长为( )
,则此四面体的棱长为( )


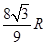

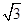 ,则该四棱台的表面积为( ).
,则该四棱台的表面积为( ).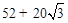
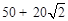
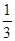 B、
B、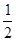 C、
C、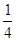 D、1
D、1