题目内容
在棱长为 的正方体
的正方体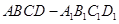 中,
中,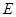 是线段
是线段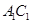 的中点,
的中点, .
.
(1) 求证: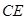 ^
^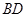 ;
;
(2) 求证: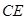 //平面
//平面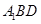 ;
;
(3) 求三棱锥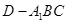 的表面积.
的表面积.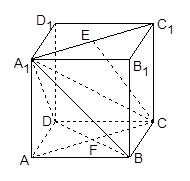
 的正方体
的正方体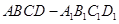 中,
中,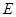 是线段
是线段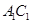 的中点,
的中点, .
.(1) 求证:
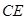 ^
^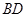 ;
;(2) 求证:
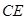 //平面
//平面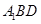 ;
;(3) 求三棱锥
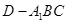 的表面积.
的表面积.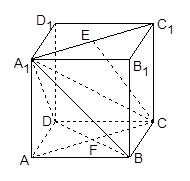
(1)证明见解析 (2) 证明见解析
(3)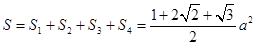 .
.
(3)
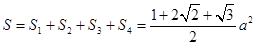 .
.本试题考查了线线垂直和线面平行的判定定理和表面积公式的运用。第一问中,利用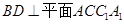 ,得到结论,第二问中,先判定
,得到结论,第二问中,先判定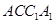 为平行四边形,然后
为平行四边形,然后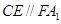 ,可知结论成立。
,可知结论成立。
第三问中,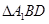 是边长为
是边长为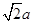 的正三角形,其面积为
的正三角形,其面积为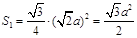 ,
,
因为 平面
平面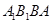 ,所以
,所以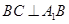 ,
,
所以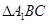 是直角三角形,其面积为
是直角三角形,其面积为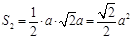 ,
,
同理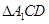 的面积为
的面积为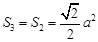 ,
,  面积为
面积为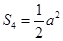 . 所以三棱锥
. 所以三棱锥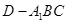 的表面积为
的表面积为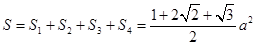 .
.
解: (1)证明:根据正方体的性质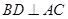 ,
,
因为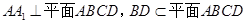 ,
,
所以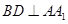 ,又
,又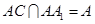 ,所以
,所以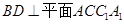 ,
,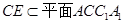 ,
,
所以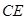 ^
^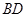 . ………………4分
. ………………4分
(2)证明:连接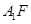 ,因为
,因为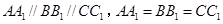 ,
,
所以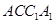 为平行四边形,因此
为平行四边形,因此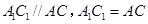 ,
,
由于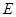 是线段
是线段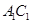 的中点,所以
的中点,所以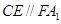 , …………6分
, …………6分
因为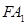
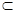 面
面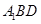 ,
,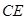
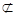 平面
平面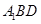 ,所以
,所以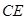 ∥平面
∥平面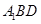 . ……………8分
. ……………8分
(3)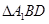 是边长为
是边长为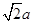 的正三角形,其面积为
的正三角形,其面积为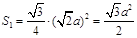 ,
,
因为 平面
平面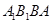 ,所以
,所以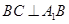 ,
,
所以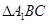 是直角三角形,其面积为
是直角三角形,其面积为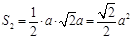 ,
,
同理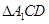 的面积为
的面积为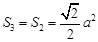 , ……………………10分
, ……………………10分
 面积为
面积为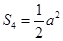 . 所以三棱锥
. 所以三棱锥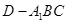 的表面积为
的表面积为
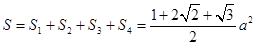
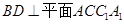 ,得到结论,第二问中,先判定
,得到结论,第二问中,先判定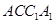 为平行四边形,然后
为平行四边形,然后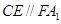 ,可知结论成立。
,可知结论成立。第三问中,
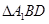 是边长为
是边长为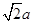 的正三角形,其面积为
的正三角形,其面积为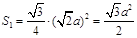 ,
,因为
 平面
平面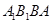 ,所以
,所以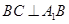 ,
,所以
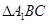 是直角三角形,其面积为
是直角三角形,其面积为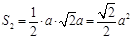 ,
,同理
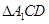 的面积为
的面积为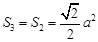 ,
,  面积为
面积为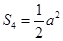 . 所以三棱锥
. 所以三棱锥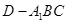 的表面积为
的表面积为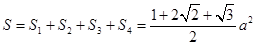 .
.解: (1)证明:根据正方体的性质
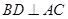 ,
,因为
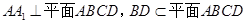 ,
,所以
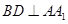 ,又
,又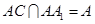 ,所以
,所以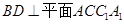 ,
,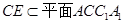 ,
,所以
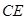 ^
^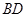 . ………………4分
. ………………4分(2)证明:连接
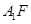 ,因为
,因为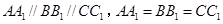 ,
,所以
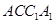 为平行四边形,因此
为平行四边形,因此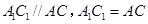 ,
,由于
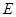 是线段
是线段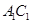 的中点,所以
的中点,所以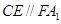 , …………6分
, …………6分因为
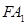
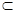 面
面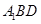 ,
,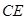
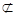 平面
平面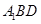 ,所以
,所以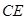 ∥平面
∥平面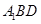 . ……………8分
. ……………8分(3)
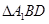 是边长为
是边长为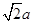 的正三角形,其面积为
的正三角形,其面积为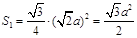 ,
,因为
 平面
平面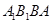 ,所以
,所以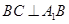 ,
,所以
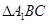 是直角三角形,其面积为
是直角三角形,其面积为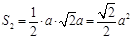 ,
,同理
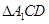 的面积为
的面积为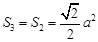 , ……………………10分
, ……………………10分 面积为
面积为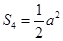 . 所以三棱锥
. 所以三棱锥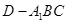 的表面积为
的表面积为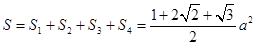

练习册系列答案
相关题目
 中,
中,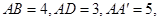 ∠
∠ ,
, =∠
=∠ ,则
,则 等于( )
等于( )





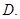

 的8个顶点都在体积为
的8个顶点都在体积为 的球面上,若
的球面上,若 ,则
,则 __________.
__________.



 二面角的平面所截,截面是一个椭圆, 则此椭圆的焦距为 .
二面角的平面所截,截面是一个椭圆, 则此椭圆的焦距为 .

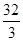 π,则该正方体的表面积为( )
π,则该正方体的表面积为( )
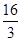
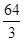
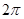 ,底面面积为
,底面面积为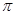 ,则该圆锥的体积为 。
,则该圆锥的体积为 。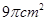 ,且它的侧面展开图是一个半圆,则圆锥的底面半径为
,且它的侧面展开图是一个半圆,则圆锥的底面半径为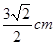

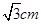
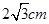 ()
()