题目内容
一个球与正三棱柱的三个侧面和两个底面都相切,已知球的体积为 ,那么该三棱柱的体积为
,那么该三棱柱的体积为
 ,那么该三棱柱的体积为
,那么该三棱柱的体积为A.16 | B.24 | C.48 | D.96 |
C
解:由球的体积公式,得4 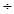 3 πR3=32π
3 πR3=32π 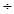 3 ,
3 ,
∴R=2.
∴正三棱柱的高h=2R=4.
设正三棱柱的底面边长为a,则其内切圆的半径为: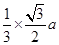 =2,
=2,
∴a=4 .
.
∴该正三棱柱的体积为:V=S底•h= •a•a•sin60°•h=
•a•a•sin60°•h= 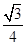 •(4
•(4 )2•4="48"
)2•4="48"  .
.
故答案为:C
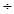 3 πR3=32π
3 πR3=32π 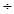 3 ,
3 ,∴R=2.
∴正三棱柱的高h=2R=4.
设正三棱柱的底面边长为a,则其内切圆的半径为:
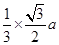 =2,
=2,∴a=4
 .
.∴该正三棱柱的体积为:V=S底•h=
 •a•a•sin60°•h=
•a•a•sin60°•h= 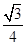 •(4
•(4 )2•4="48"
)2•4="48"  .
.故答案为:C

练习册系列答案
相关题目
 中,底面
中,底面 是直角梯形,
是直角梯形,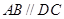 ,
,
 ,
,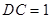 ,
, ,
, 平面
平面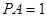 .
. 平面
平面 ;
; 平面
平面 ;
;  是
是 的中点,求三棱锥
的中点,求三棱锥 的体积.
的体积. 为梯形,
为梯形, ,
, ,求图中阴影部分绕
,求图中阴影部分绕 旋转一周所形成的几何体的表面积和体积。
旋转一周所形成的几何体的表面积和体积。
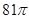
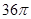
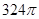
 中,
中,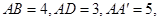 ∠
∠ ,
, =∠
=∠ ,则
,则 等于( )
等于( )





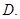

 二面角的平面所截,截面是一个椭圆, 则此椭圆的焦距为 .
二面角的平面所截,截面是一个椭圆, 则此椭圆的焦距为 .
 、
、 、
、 ,则这个长方体的外接球的表面积为 .
,则这个长方体的外接球的表面积为 . ,AB为直径,C是圆周上一点,且
,AB为直径,C是圆周上一点,且 ,平面
,平面 平面
平面 ,
, ,
,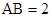 ,
, ,设直线PC与平面
,设直线PC与平面 、
、 的大小为
的大小为 ,则
,则



