题目内容
如图所示，PA⊥平面ABCD，四边形ABCD为正方形，且2PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.
（Ⅰ）求异面直线EF与AG所成角的余弦值；
（Ⅱ）求证：BC∥面EFG；
（Ⅲ）求三棱锥E-AFG的体积.
（Ⅰ）求异面直线EF与AG所成角的余弦值；
（Ⅱ）求证：BC∥面EFG；
（Ⅲ）求三棱锥E-AFG的体积.
Ⅰ）解：因为E,F分别是PA,PD的中点，所以EF∥AD,
于是，∠DAG是EF与AG所成的角．．．．．．．．．．．．．．．．．．．．2分
EF与AG所成角的余弦值是
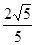．．．．．．．．．．．．．．．．．．4分
（Ⅱ）因为BC∥AD,AD∥EF,所以BC∥EF．．．．．．．．．．6分
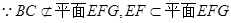
∥平面EFG．．．．．．．．．．．．8分
（Ⅲ）VE-AFG=VG-AEF=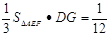
于是，∠DAG是EF与AG所成的角．．．．．．．．．．．．．．．．．．．．2分
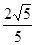EF与AG所成角的余弦值是．．．．．．．．．．．．．．．．．．4分（Ⅱ）因为BC∥AD,AD∥EF,所以BC∥EF．．．．．．．．．．6分
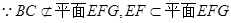
∥平面EFG．．．．．．．．．．．．8分（Ⅲ）VE-AFG=VG-AEF=
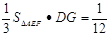
(I)求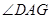
即可.
(2)证明BC//AD//EF.
1. 根据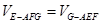
转化成求三棱锥G-AEF的体积.
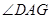即可.(2)证明BC//AD//EF.
1. 根据
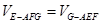转化成求三棱锥G-AEF的体积.
练习册系列答案
相关题目
中，底面
是直角梯形，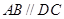
，
，
，
，
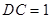平面
．
平面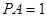
；
平面
； 
是
的中点，求三棱锥
的体积．
二面角的平面所截，截面是一个椭圆， 则此椭圆的焦距为 .
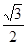
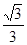
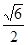
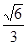
三点的截面和球心的距离为球半径的一半，且
，则球的表面积为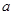 
的正方体外接球的表面积为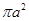
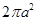
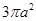
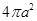
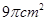，且它的侧面展开图是一个半圆，则圆锥的底面半径为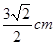
（）
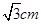
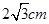