题目内容
【题目】已知数列{an}中，a1=3，a2=5，其前n项和为Sn满足Sn+Sn﹣2=2Sn﹣1+2n﹣1（n≥3，n∈N*）
（1）试求数列{an}的通项公式
（2）令bn= 
，Tn是数列{bn}的前n项和．证明：对任意给定的m∈（0， 
），均存在n0∈N*，使得当n≥n0时，Tn＞m恒成立．
【答案】
（1）解：由Sn+Sn﹣2=2Sn﹣1+2n﹣1（n≥3，n∈N*），整理得：Sn﹣Sn﹣1=Sn﹣1﹣Sn﹣2+2n﹣1，
∴an=an﹣1=2n﹣1，即an﹣an﹣1=2n﹣1，n≥3，
∵a2﹣a1=2，
a3﹣a2=4，
a4﹣a3=23，
…
an﹣an﹣1=2n﹣1，
将上式累加整理得：an﹣a1=2+4+23+…+2n﹣1，
∴an= 
+3=2n+1，
数列{an}的通项公式an=2n+1；
（2）证明： bn= 
= 
= 
（ 
﹣ 
），
∴数列{bn}的前n项和Tn=b1+b2+b3+…+bn，
= [（ 
﹣ 
）+（ ﹣ 
）+…+（ ﹣ ）]，
= （ ﹣ ），
Tn+1﹣Tn= 
＞0，
∴Tn随着n的增大而增大，
若Tn＞m，则 （ ﹣ ）＞m，化简整理得： 
＞ ，
∵m∈（0， 
），
∴1﹣6m＞0，
∴2n+1＞ 
﹣1，
n＞log2（ ﹣1）﹣1，
当log2（ ﹣1）﹣1＜1时，即0＜m＜ 
，取n0=1，
当log2（ ﹣1）﹣1≥1时，解得： ≤m＜ ，记log2（ ﹣1）﹣1的整数部分为p，
取n0=p+1即可，
综上可知，对任意m∈（0， ），均存在n0∈N*，使得当n≥n0时，Tn＞m恒成立
【解析】（1）由题意可知Sn﹣Sn﹣1=Sn﹣1﹣Sn﹣2+2n﹣1 ， 即an﹣an﹣1=2n﹣1 ， n≥3，采用“累加法”即可求得数列{an}的通项公式；（2）由（1）可知，bn= = = （ ﹣ ），采用“裂项法”即可求得数列{bn}的前n项和Tn ， 由函数的单调性可知，Tn随着n的增大而增大，分离参数n＞log2（ ﹣1）﹣1，分类log2（ ﹣1）﹣1＜1及log2（ ﹣1）﹣1≥1时，求得m的取值范围，求得n0的值，即可证明存在n0∈N*，使得当n≥n0时，Tn＞m恒成立．
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点，需要掌握数列{an}的前n项和sn与通项an的关系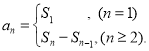
；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式才能正确解答此题．
