题目内容
16.若不等式x2+2xy≤a(x2+y2)对于一切正数x,y恒成立,则实数a的最小值为$\frac{\sqrt{5}+1}{2}$.分析 由题意可得a≥$\frac{{x}^{2}+2xy}{{x}^{2}+{y}^{2}}$的最大值,由x2+y2=(1-m2)x2+m2x2+y2(m>0),运用基本不等式,及解方程1-m2=m,可得m,进而得到a的最小值.
解答 解:由题意可得a≥$\frac{{x}^{2}+2xy}{{x}^{2}+{y}^{2}}$的最大值,
由x2+y2=(1-m2)x2+m2x2+y2(m>0)
≥(1-m2)x2+2mxy,(当且仅当mx=y取得等号),
则$\frac{{x}^{2}+2xy}{{x}^{2}+{y}^{2}}$≤$\frac{{x}^{2}+2xy}{(1-{m}^{2}){x}^{2}+2mxy}$,
当1-m2=m,即m=$\frac{\sqrt{5}-1}{2}$时,$\frac{{x}^{2}+2xy}{{x}^{2}+{y}^{2}}$的最大值为$\frac{2}{\sqrt{5}-1}$=$\frac{\sqrt{5}+1}{2}$.
即有a≥$\frac{\sqrt{5}+1}{2}$.
故答案为:$\frac{\sqrt{5}+1}{2}$.
点评 本题考查基本不等式在最值问题中的运用,注意变形以及等号成立的条件,考查运算能力,属于中档题.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
6.命题P:?x∈R,$x+\frac{1}{x}<a$成立,则P的否定为( )
| A. | ?x∈R,$x+\frac{1}{x}>a$成立 | B. | ?x∈R,$x+\frac{1}{x}<a$成立 | C. | ?x∈R,$x+\frac{1}{x}≥a$成立 | D. | ?x∈R,$x+\frac{1}{x}≤a$成立 |
8.一个球的体积等于其表面积,那么这个球的半径为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 3 |
6.几何体的三视图和相关数据如图所示,则该几何体的体积为( )
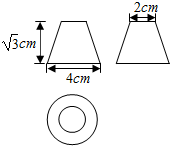

| A. | $\frac{{7\sqrt{3}π}}{3}$ | B. | $\frac{{8\sqrt{3}π}}{3}$ | C. | $\frac{7π}{3}$ | D. | $\frac{8π}{3}$ |