Question

15．已知圆x²+y²-2y-3=0经过椭圆的两个焦点，且与该椭圆只有一个交点，求该椭圆的标准方程．

Answer 1

分析 由题意设出椭圆方程，求解圆与x轴的交点得c，画出图形，数形结合可得b，再由隐含条件求得a，则椭圆的标准方程可求．

解答 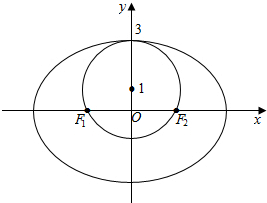解：圆的方程x²+y²-2y-3=0化为标准式为x²+（y-1）²=4，可知圆心（0，1），半径为2，
设椭圆的标准方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1（a＞b＞0）$，
在方程x²+（y-1）²=4中取y=0，可得x=$±\sqrt{3}$，
∴c=$\sqrt{3}$，即a²-b²=3，
又∵圆与椭圆只有一个交点，
如图可得b=3，
∴a²=12．
∴椭圆的标准方程为$\frac{{x}^{2}}{12}+\frac{{y}^{2}}{9}=1$．

点评 本题考查椭圆标准方程的求法，考查了数形结合的解题思想方法，是中档题．