Question

3．已知0＜x＜1，-1＜y＜1，则x-y的取值范围是（-1，2），$\frac{y+1}{x+1}$的取值范围是[0，2]．

Answer 1

分析 （1）利用不等式的基本性质即可得出；（2）画出满足条件的平面区域，结合$\frac{y+1}{x+1}$的几何意义，求出其范围即可．

解答 解：（1）∵-1＜y＜1，∴-1＜y＜1，
∵0＜x＜1，
∴-1＜x-y＜1．
∴x-y的取值范围是（-1，2），
故答案为：（-1，2）；
（2）画出满足0＜x＜1，-1＜y＜1的平面区域，
如图示：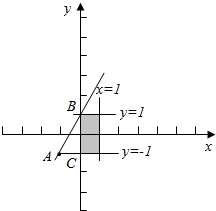
，
$\frac{y+1}{x+1}$表示过平面区域内的点和点A（-1，-1）的直线的斜率，
显然直线过AB时，斜率最大是：2，直线过AC时，斜率最小是0，
故答案为：[0，2]．

点评 本题考查了基本不等式的性质，考查简单的线性规划问题，是一道基础题．