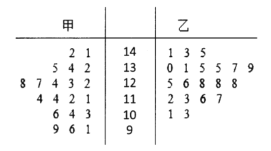
题目内容
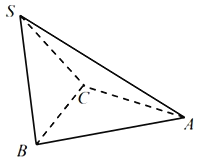
【题目】如图所示，三棱锥S一ABC中，△ABC与△SBC都是边长为1的正三角形，二面角A﹣BC﹣S的大小为
，若S，A，B，C四点都在球O的表面上，则球O的表面积为（ ）
A.
πB.
πC.
πD.3π
【答案】A
【解析】
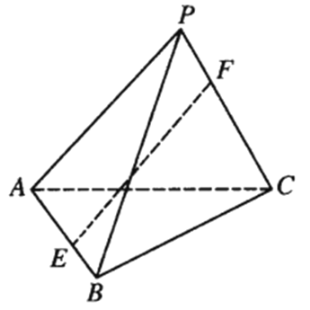
取线段BC的中点D，连结AD，SD，由题意得AD⊥BC，SD⊥BC，∠ADS是二面角A﹣BC﹣S的平面角，∠ADS
，由题意得BC⊥平面ADS，分别取AD，SD的三等分点E，F，在平面ADS内，过点E，F分别作直线垂直于AD，SD，两条直线的交点即球心O，连结OA，则球O半径R＝|OA|，由此能求出球O的表面积．
解：取线段BC的中点D，连结AD，SD，
由题意得AD⊥BC，SD⊥BC，
∴∠ADS是二面角A﹣BC﹣S的平面角，∴∠ADS，
由题意得BC⊥平面ADS，
分别取AD，SD的三等分点E，F，
在平面ADS内，过点E，F分别作直线垂直于AD，SD，
两条直线的交点即球心O，
连结OA，则球O半径R＝|OA|，
由题意知BD
，AD
，DE
，AE
，
连结OD，在Rt△ODE中，
，OE
DE，
∴OA2＝OE2+AE2
，
∴球O的表面积为S＝4πR2
．
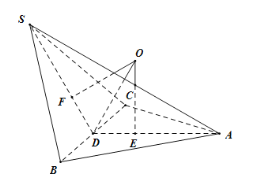
故选：A．
练习册系列答案
一本好题口算题卡系列答案
相关题目
