题目内容
【题目】某数学教师在甲、乙两个平行班采用“传统教学”和“高效课堂”两种不同的教学模式进行教学实验.为了解教改实效，期中考试后，分别从两个班中各随机抽取
名学生的数学成绩进行统计，得到如下的茎叶图：
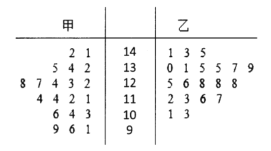
（1）求甲、乙两班抽取的分数的中位数，并估计甲、乙两班数学的平均水平和分散程度（不要求计算出具体值，给出结论即可）；
（2）若规定分数在
的为良好，现已从甲、乙两班成绩为良好的同学中，用分层抽样法抽出
位同学参加座谈会，要再从这位同学中任意选出
人发言，求这人来自不同班的概率.
【答案】（1）甲班抽出同学数学分数的中位数：
；乙班抽出同学数学分数的中位数：
；乙班学生数学考试分数的平均水平高于甲班学生数学考试分数的平均水平；甲班学生数学考试分数的分散程度高于乙班学生数学考试分数的分散程度（2）
【解析】
（1）由茎叶图求出中位数，再观察数据估计甲、乙两班数学的平均水平和分散程度即可；
（2）用分层抽样法抽出
人，则应从甲、乙两班各抽出
人、
人，然后列举出其基本事件，然后利用古典概型概率公式求解即可.
解：（1）根据茎叶图得：
甲班抽出同学数学分数的中位数：
，
乙班抽出同学数学分数的中位数：
.
乙班学生数学考试分数的平均水平高于甲班学生数学考试分数的平均水平；
甲班学生数学考试分数的分散程度高于乙班学生数学考试分数的分散程度.
（2）根据茎叶图可知：
甲、乙两班数学成绩为良好的人数分别为
、
，
若用分层抽样法抽出人，则应从甲、乙两班各抽出人、人.
设“位同学任意选出人发言，这人是来自不同班的同学”为事件
.
将甲班选出的人记为：
、
、
，乙班选出的人记为：
.则共有“
、
、
、
、
、
”种选法，事件包含“、、”种.
故
.
故选出的人是来自不同班的同学的概率等于.
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
