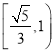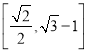Question

【题目】已知数列{an}满足，an+2＝3an+1﹣2an，a1＝1，a2＝3，记bn，Sn为数列{bn}的前n项和.

（1）求证：{an+1﹣an}为等比数列，并求an；

（2）求证：Sn.

Answer 1

【答案】（1）证明见解析；an＝2n﹣1，n∈N*；（2）证明见解析

【解析】

(1)将题干中递推公式进行转化可得，从而可证得数列{an+1﹣an}是以2为首项，2为公比的等比数列，则有，n∈N*.然后根据此递推公式的特点运用累加法可计算出数列{an}的通项公式；

(2)先根据第(1)题的结果计算出数列{bn}的通项公式，然后运用数学归纳法证明不等式成立，注意在具体证明过程中运用分析法证明根式不等式成立，综合即可证得不等式成立.

证明：（1）依题意，由an+2＝3an+1﹣2an，可得：

，

∵a2﹣a1＝3﹣1＝2，

∴数列{an+1﹣an}是以2为首项，2为公比的等比数列，

∴，n∈N*.

故a1＝1，

a2﹣a1＝21，

a3﹣a2＝22，

…

an﹣an﹣1＝2n﹣1，

各项相加，可得

an＝1+21+22+…+2n﹣12n﹣1，n∈N*.

（2）由（1）知，bn，

下面用数学归纳法证明不等式成立，

①当n＝1时，S1＝b1，

∵右边，

要证明：，

只要证明：2，

两边平方，可得，

化简整理，得27，

∵（2）2＝40＜72＝49，

∴成立，

即当n＝1时，不等式成立.

②假设当n＝k时，不等式成立，即Sk，

则当n＝k+1时，，

要证明：Sk+1，

只要证明：，

，

化简，得，

两边平方，可得（）2≤（）2，

化简整理，得3k+7，

两边平方，可得（3k+4）（3k+10）≤（3k+7）2，

化简整理，得9k2+42k+40≤9k2+42k+49，

∵40＜49，

∴9k2+42k+40≤9k2+42k+49成立，

∴成立，

即：Sk+1成立，

∴当n＝k+1时，不等式也成立.

综上所述，可得

对n∈N*成立，故得证.