题目内容
【题目】已知数列![]() 、
、![]() 满足
满足![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)设数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证:![]() ;
;
(Ⅲ)设数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:当
,求证:当![]() 时,
时,![]() .
.
【答案】(Ⅰ)证明见解析;(Ⅱ)证明见解析;(Ⅲ)证明见解析.
【解析】
(Ⅰ)推导出数列![]() ,可得出
,可得出![]() ,利用基本不等式可得出
,利用基本不等式可得出![]() ,再由
,再由![]() 可得出
可得出![]() ,利用作差法证得
,利用作差法证得![]() ,进而可证得结论;
,进而可证得结论;
(Ⅱ)由![]() 可得出
可得出![]() ,结合
,结合![]() 可推导出
可推导出![]() ,进而得出
,进而得出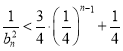 ,再利用放缩法可证得结论成立;
,再利用放缩法可证得结论成立;
(Ⅲ)由![]() 可推导出
可推导出![]() ,进而可得出
,进而可得出![]() ,再利用累加法及等比数列的求和公式即可证明.
,再利用累加法及等比数列的求和公式即可证明.
(Ⅰ)因为![]() ,则
,则![]() 为常数数列,
为常数数列,
又![]() ,
,![]() ,且
,且![]() ,则
,则![]() ,
,
故![]() ,
,![]() ,易知
,易知![]() ,
,
所以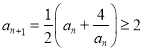 (当且仅当
(当且仅当![]() 时取等号),
时取等号),
因为![]() ,因此
,因此![]() .
.
又![]() ,所以
,所以![]() ;
;
(Ⅱ)由![]() ,有
,有![]() ,
,
又![]() ,则
,则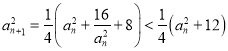 ,则
,则![]() ;
;
故![]() ,即
,即![]() ,
,
所以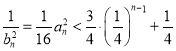 ,
,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,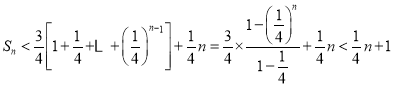
![]() ,
,
因此,![]() 的前
的前![]() 项和
项和![]() ;
;
(Ⅲ)由![]() ,得
,得![]() ,
,
又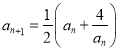 ,则
,则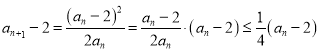 ,故
,故![]() ,
,
所以![]()
![]() ,
,
因此,![]() 的前
的前![]() 项和
项和![]() .
.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目