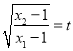题目内容
【题目】在平面四边形ABCD中,AB=8,AD=5,CD=![]() ,∠A=
,∠A=![]() ,∠D=
,∠D=![]() .
.
(Ⅰ)求△ABD的内切圆的半径;
(Ⅱ)求BC的长.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】试题分析:(Ⅰ)在△ABD中,由余弦定理,得![]() ,设△ABD的内切圆的半径为r,
,设△ABD的内切圆的半径为r,
由![]() 可求得
可求得![]() (Ⅱ)连接BD,由已知,利用余弦定理可求BD的值,进而可求cos∠ADB的值,利用两角差的余弦函数公式可求cos∠BDC的值,进而利用余弦定理即可得解BC的值.
(Ⅱ)连接BD,由已知,利用余弦定理可求BD的值,进而可求cos∠ADB的值,利用两角差的余弦函数公式可求cos∠BDC的值,进而利用余弦定理即可得解BC的值.
试题解析:
(Ⅰ)在△ABD中,AB=8,AD=5,∠A=![]() ,
,

由余弦定理,得![]()
设△ABD的内切圆的半径为r,
由![]() ,
,
得![]() ,解得
,解得![]() .
.
(Ⅱ)设∠ADB= ![]() ,∠BDC=
,∠BDC= ![]() ,则
,则![]() .
.
在△ABD中,由余弦定理,得![]()
又![]() ,∴
,∴![]()
∴![]() ,
,
在△BDC中,CD=![]() ,由余弦定理,得
,由余弦定理,得
![]()

练习册系列答案
相关题目
【题目】某花店每天以每枝![]() 元的价格从农场购进若干枝玫瑰花,然后以每枝
元的价格从农场购进若干枝玫瑰花,然后以每枝![]() 元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(I)若花店一天购进![]() 枝玫瑰花,写出当天的利润
枝玫瑰花,写出当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:枝,
(单位:枝, ![]() )的函数解析式.
)的函数解析式.
(II)花店记录了![]() 天玫瑰花的日需求量(单位:枝),整理得下表:
天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
以![]() 天记录的各需求量的频率作为各需求量发生的概率.
天记录的各需求量的频率作为各需求量发生的概率.
(i)若花店一天购进![]() 枝玫瑰花,
枝玫瑰花, ![]() 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求![]() 的分布列,数学期望.
的分布列,数学期望.
(ii)若花店计划一天购进![]() 枝或
枝或![]() 枝玫瑰花,你认为应购进
枝玫瑰花,你认为应购进![]() 枝还是
枝还是![]() 枝?只写结论.
枝?只写结论.