题目内容
【题目】已知数列{an}的首项![]() ,
, ![]() ,
, ![]() .
.
(1)求证:数列 为等比数列;
为等比数列;
(2)记![]() ,若Sn<100,求最大正整数n;
,若Sn<100,求最大正整数n;
(3)是否存在互不相等的正整数m,s,n,使m,s,n成等差数列,且am-1,as-1,an-1成等比数列?如果存在,请给以证明;如果不存在,请说明理由.
【答案】(1)见解析;(2)99;(3)不存在
【解析】试题分析:(1)根据![]() 可得
可得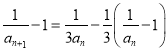 ,根据
,根据![]() ,可知
,可知![]() ,即
,即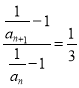 ,据此即可求证;(2)根据等比数列的通项公式可得
,据此即可求证;(2)根据等比数列的通项公式可得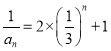 ,进而即可表示出
,进而即可表示出![]() ,对其进行整理可得
,对其进行整理可得![]() ,由于
,由于![]() ,所以有
,所以有![]() ,即
,即![]() ,至此,即可得到最大正整数
,至此,即可得到最大正整数![]() ;(3)首先假设存在,根据等差数列的性质可得
;(3)首先假设存在,根据等差数列的性质可得![]() ,再根据等比的性质可得
,再根据等比的性质可得![]() ,结合(2)中得到的通项公式可将其化简为
,结合(2)中得到的通项公式可将其化简为![]() ,接下来再根据均值不等式可知
,接下来再根据均值不等式可知![]() ,当且仅当
,当且仅当![]() 时等号成立,至此,再根据
时等号成立,至此,再根据![]() 互不相等即可得结果.
互不相等即可得结果.
试题解析:(1)因为![]() =
=![]() +
+![]() ,所以
,所以![]() -1=
-1=![]() -
-![]() .又因为
.又因为![]() -1≠0,所以
-1≠0,所以![]() -1≠0(n∈N*).
-1≠0(n∈N*).
所以数列![]() 为等比数列.
为等比数列.
(2)由(1)可得![]() -1=
-1=![]() ·
·![]() n-1,所以
n-1,所以![]() =2·
=2·![]() n+1.
n+1.
Sn=![]() +
+![]() +…+
+…+![]() =n+2
=n+2![]() =n+2·
=n+2·![]() =n+1-
=n+1-![]() ,
,
若Sn<100,则n+1-![]() <100,因为函数y= n+1-
<100,因为函数y= n+1-![]() 单调增, 所以最大正整数n的值为99.
单调增, 所以最大正整数n的值为99.
(3)假设存在,则m+n=2s,(am-1)(an-1)=(as-1)2,
因为an=![]() ,所以
,所以![]()
![]() =
=![]() 2,
2,
化简得3m+3n=2·3s,因为3m+3n≥2·![]() =2·3s,
=2·3s,
当且仅当m=n时等号,又m,s,n互不相等,所以不存在.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案【题目】随着我国经济的快速发展,民用汽车的保有量也迅速增长.机动车保有量的发展影响到环境质量、交通安全、道路建设等诸多方面.在我国,尤其是大中型城市,机动车已成为城市空气污染的重要来源.因此,合理预测机动车保有量是未来进行机动车污染防治规划、道路发展规划等的重要前提.从2012年到2016年,根据“云南省某市国民经济和社会发展统计公报”中公布的数据,该市机动车保有量数据如表所示.
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
机动车保有量 | 169 | 181 | 196 | 215 | 230 |
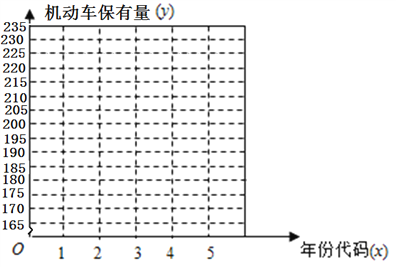
(1)在图所给的坐标系中作出数据对应的散点图;
(2)建立机动车保有量![]() 关于年份代码
关于年份代码![]() 的回归方程;
的回归方程;
(3)按照当前的变化趋势,预测2017年该市机动车保有量.
附注:回归直线方程![]() 中的斜率和截距的最小二乘估计公式分别为:
中的斜率和截距的最小二乘估计公式分别为:
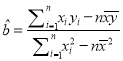 ,
, ![]() .
.