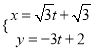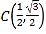题目内容
【题目】函数![]() ,其图象与
,其图象与![]() 轴交于
轴交于![]() ,
, ![]() 两点,且
两点,且![]() .
.
(Ⅰ)求![]() 的取值范围;
的取值范围;
(Ⅱ)证明: ![]() (
(![]() 为
为![]() 的导函数).
的导函数).
(Ⅲ)设点![]() 在函数
在函数![]() 图象上,且
图象上,且![]() 为等腰直角三角形,记
为等腰直角三角形,记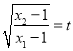 ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]()
【解析】试题分析:(1)根据题意图象与![]() 轴交于
轴交于![]() ,
, ![]() 两点,由零点的定义可得:函数的图象要与x轴有两个交点,而此函数的特征不难发现要对它进行求导,运用导数与函数的关系进行求函数的性质,即:
两点,由零点的定义可得:函数的图象要与x轴有两个交点,而此函数的特征不难发现要对它进行求导,运用导数与函数的关系进行求函数的性质,即: ![]() ,a的正负就决定着导数的取值情况,故要对a进行分类讨论:分
,a的正负就决定着导数的取值情况,故要对a进行分类讨论:分![]() 和
和![]() 两种情况,其中
两种情况,其中![]() 显然不成立,
显然不成立, ![]() 时转化为函数的最小值小于零,即可求出a的范围; (2)由图象与
时转化为函数的最小值小于零,即可求出a的范围; (2)由图象与![]() 轴交于
轴交于![]() ,
, ![]() 两点,结合零点的定义可得:
两点,结合零点的定义可得: ![]() 整理可得:
整理可得: ![]() ,观察其结构特征,可想到整体思想,即:
,观察其结构特征,可想到整体思想,即: ![]() ,目标为:
,目标为: ![]() ,运用整体代入化简可得:
,运用整体代入化简可得:  ,转化为对函数
,转化为对函数![]() 进行研究,运用导数知识不难得到
进行研究,运用导数知识不难得到![]() ,即:
,即: ![]() ,故而
,故而![]() 是单调增函数,由不等式知:
是单调增函数,由不等式知: ![]() ,问题可得证; (3)由题意有
,问题可得证; (3)由题意有![]() ,化简得
,化简得![]()
![]()
![]() ,而在等腰三角形ABC中,显然只有C= 90°,这样可得
,而在等腰三角形ABC中,显然只有C= 90°,这样可得![]() ,即
,即![]() ,结合直角三角形斜边的中线性质,可知
,结合直角三角形斜边的中线性质,可知![]() ,所以
,所以![]() ,即
,即![]() ,运用代数式知识处理可得:
,运用代数式知识处理可得: 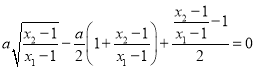 ,而
,而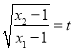 ,所以
,所以![]() ,即
,即![]() ,所求得
,所求得![]()
试题解析:(1)![]() .
.
若![]() ,则
,则![]() ,则函数
,则函数![]() 是单调增函数,这与题设矛盾.
是单调增函数,这与题设矛盾.
所以![]() ,令
,令![]() ,则
,则![]() .
.
当![]() 时,
时, ![]() ,
, ![]() 是单调减函数;
是单调减函数; ![]() 时,
时, ![]() ,
, ![]() 是单调增函数;
是单调增函数;
于是当![]() 时,
时, ![]() 取得极小值.
取得极小值.
因为函数![]() 的图象与
的图象与![]() 轴交于两点
轴交于两点![]() ,
, ![]() (x1<x2),
(x1<x2),
所以![]() ,即
,即![]()
此时,存在![]() ;
;
存在![]()
![]() ,
,
又由![]() 在
在![]() 及
及![]() 上的单调性及曲线在R上不间断,可知
上的单调性及曲线在R上不间断,可知![]() 为所求取值范围.
为所求取值范围.
(2)因为![]() 两式相减得
两式相减得![]()
记![]() ,则
,则 ,
,
设![]() ,则
,则![]() ,所以
,所以![]() 是单调减函数,
是单调减函数,
则有![]() ,而
,而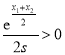 ,所以
,所以![]() .
.
又![]() 是单调增函数,且
是单调增函数,且![]()
所以![]() .
.
(3)依题意有![]() ,则
,则![]()
![]()
![]() .
.
于是![]() ,在等腰三角形ABC中,显然C= 90°, 13分
,在等腰三角形ABC中,显然C= 90°, 13分
所以![]() ,即
,即![]() ,
,
由直角三角形斜边的中线性质,可知![]() ,
,
所以![]() ,即
,即![]() ,
,
所以![]() ,
,
即![]() .
.
因为![]() ,则
,则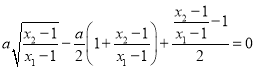 ,
,
又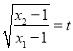 ,所以
,所以![]() ,
,
即![]() ,所以
,所以![]()