题目内容
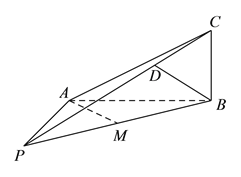
【题目】如图,在四棱柱![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() .点
.点![]() 在棱
在棱![]() 上,平面
上,平面![]() 与棱
与棱![]() 相交于点
相交于点![]() .
.
(Ⅰ)求证: ![]() 平面
平面![]() .
.
(Ⅱ)求证: ![]() 平面
平面![]() .
.
(Ⅲ)求三棱锥![]() 的体积的取值范围.
的体积的取值范围.

【答案】(Ⅰ)见解析(Ⅱ)见解析(Ⅲ)![]()
【解析】试题分析:(Ⅰ)由题意证得![]() 根据线面平行的判定定理即可证明A1F∥平面B1CE;
根据线面平行的判定定理即可证明A1F∥平面B1CE;
(Ⅱ)由题意证得![]() ,根据线面垂直的判定定理即可证明AC⊥平面CDD1C1;(Ⅲ)根据
,根据线面垂直的判定定理即可证明AC⊥平面CDD1C1;(Ⅲ)根据![]() ,
, ![]() 为定值,即为
为定值,即为![]() 长度为
长度为![]() ,而
,而![]() ,由题意得
,由题意得![]() 即求得三棱锥
即求得三棱锥![]() 体积的范围.
体积的范围.
试题解析:
(Ⅰ)∵在棱柱![]() 中,
中,
平面![]() 平面
平面![]() ,
,
又∵平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅱ)在底面![]() 中,
中,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
, ![]() ,
,
∵![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
∴![]() ,
,
在四棱柱![]() 中,
中,
![]() ,
,
∴![]() ,
,
∵![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅲ)![]()
![]() ,
,
∵![]() 为定值,即为
为定值,即为![]() 长度为
长度为![]() .
.
而![]() ,过
,过![]() 点作
点作![]() ,
,
∴![]() ,
,
∵![]() 长度界于
长度界于![]() 与
与![]() 之间,
之间,
即![]() ,
,
∴![]()
![]()
![]() ,
,
∴三棱锥![]() 体积在
体积在![]() 间.
间.
即三棱锥![]() 的体积的取值范围
的体积的取值范围![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目