题目内容
7.已知向量$\overrightarrow{OA}$=(k,12),$\overrightarrow{OB}$=(4,5),$\overrightarrow{OC}$=(-k,10),且A、B、C三点共线,则k=( )| A. | -$\frac{4}{3}$ | B. | $\frac{4}{3}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
分析 利用向量的坐标运算、向量共线定理即可得出.
解答 解:∵$\overrightarrow{AB}$=$\overrightarrow{OB}-\overrightarrow{OA}$=(4-k,-7),
$\overrightarrow{BC}$=$\overrightarrow{OC}-\overrightarrow{OB}$=(-k-4,5).
又A、B、C三点共线,
∴-7(-k-4)-5(4-k)=0,
解得k=$-\frac{2}{3}$.
故选:C.
点评 本题考查了向量的坐标运算、向量共线定理,属于基础题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
17.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,P是椭圆上一点,|PF1|=|F1F2|且cos∠PF2F1=$\frac{2}{3}$,则椭圆离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{7}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
2. 如图,三棱柱ABC-A1B1C1的侧棱垂直于底面,底面边长和侧棱长均为2,D是BC的中点.
如图,三棱柱ABC-A1B1C1的侧棱垂直于底面,底面边长和侧棱长均为2,D是BC的中点.
(Ⅰ)求证:AD⊥平面B1BCC1;
(Ⅱ)求证:A1B∥平面ADC1;
(Ⅲ)求三棱锥C1-ADB1的体积.
 如图,三棱柱ABC-A1B1C1的侧棱垂直于底面,底面边长和侧棱长均为2,D是BC的中点.
如图,三棱柱ABC-A1B1C1的侧棱垂直于底面,底面边长和侧棱长均为2,D是BC的中点.(Ⅰ)求证:AD⊥平面B1BCC1;
(Ⅱ)求证:A1B∥平面ADC1;
(Ⅲ)求三棱锥C1-ADB1的体积.
19.等比数列{an}中,任意的n∈N*,an+1+an=3n+1,则公比q等于( )
| A. | 2 | B. | 3 | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
17.已知椭圆C1与抛物线C2的焦点均在x轴上,C1的中心和C2的顶点为原点O,从椭圆C1上取两个点,从椭圆C2上取一个点,将其坐标记录于表中:
(1)试判断两个点在C1上,并求出C1,C2的标准方程;
(2)已知直线l:x=my+1与椭圆C2相交于不同两点M,N,且满足$\overrightarrow{OM}⊥\overrightarrow{ON}$,求参数m的值.
| x | $\sqrt{2}$ | 2 | 4 |
| y | $\frac{\sqrt{2}}{2}$ | 0 | 4 |
(2)已知直线l:x=my+1与椭圆C2相交于不同两点M,N,且满足$\overrightarrow{OM}⊥\overrightarrow{ON}$,求参数m的值.
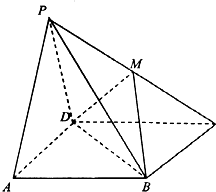 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA=PD=4,底面ABCD是边长为4的正方形,若M为PC的中点.
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA=PD=4,底面ABCD是边长为4的正方形,若M为PC的中点.