题目内容
16.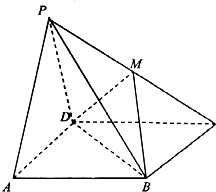 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA=PD=4,底面ABCD是边长为4的正方形,若M为PC的中点.
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA=PD=4,底面ABCD是边长为4的正方形,若M为PC的中点.(1)求证:PA∥平面BDM;
(2)求三棱锥P-BCD的体积;
(3)在AB上是否存在一个点N,使MN⊥平面PCD,若存在,试确定N的位置;若不存在请说明理由.
分析 (1)在平面BDM内找与PA平行的直线即可;
(2)取AD的中点Q,证明PQ⊥平面ABCD,利用体积公式,求三棱锥P-BCD的体积;
(3)N为AB中点时,MN⊥平面PCD,利用线面垂直的评定定理,即可得出结论.
解答 (1)证明:AC与BD的交点O,连结MO,
∵底面ABCD为矩形,
∴O为AC的中点,
又M是AC的中点,
∴MO∥PA,
又PA?平面BDM,MO?平面BDM,
∴PA∥平面BDM;
(2)解:取AD的中点Q,
∵PA=PD,
∴PQ⊥AD,
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴PQ⊥平面ABCD,
∵PA=PD=AD=4,
∴PQ=2$\sqrt{3}$,
∵底面ABCD是边长为4的正方形,
∴S△BCD=$\frac{1}{2}×4×4$=8,
∴VP-BCD=$\frac{1}{3}×8×2\sqrt{3}$=$\frac{16\sqrt{3}}{3}$;
(3)解:N为AB中点时,MN⊥平面PCD,
N为AB中点时,取PD的中点R,连接MN,MR,AR,
∴RM∥$\frac{1}{2}$DC,AN∥$\frac{1}{2}DC$,
∴RM∥AN且RM=AN,
∴四边形ANMR是平行四边形,
∴AR∥NM,
由(2)PQ⊥平面ABCD,∴PQ⊥CD,
∵CD⊥AD,PQ∩AD=Q,
∴CD⊥平面PAD,
∵AR?平面PAD,∴CD⊥AR,
∴PA=PD=AD=4,R为PD的中点,
∴AR⊥PD,
∴AR⊥平面PCD,
∵AR∥NM,
∴MN⊥平面PCD,
∴N为AB中点时,MN⊥平面PCD.
点评 本题主要考查线面垂直的判定与性质,线面平行的判定与性质,考查三棱锥体积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.已知向量$\overrightarrow{OA}$=(k,12),$\overrightarrow{OB}$=(4,5),$\overrightarrow{OC}$=(-k,10),且A、B、C三点共线,则k=( )
| A. | -$\frac{4}{3}$ | B. | $\frac{4}{3}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
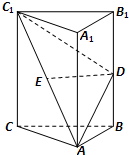 如图,在直三棱柱ABC-A1B1C1中,AB=BC,D,E分别为BB1,AC1的中点.
如图,在直三棱柱ABC-A1B1C1中,AB=BC,D,E分别为BB1,AC1的中点.