题目内容
【题目】已知数列{an}是等差数列,Sn为{an}的前n项和,且a10=19,S10=100;数列{bn}对任意n∈N* , 总有b1b2b3…bn﹣1bn=an+2成立.
(1)求数列{an}和{bn}的通项公式;
(2)记cn=(﹣1)n ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
【答案】
(1)
解:设{an}的公差为d,
则a10=a1+9d=19, ![]() ,
,
解得a1=1,d=2,所以an=2n﹣1,
所以b1b2b3…bn﹣1bn=2n+1…①
当n=1时,b1=3,
当n≥2时,b1b2b3…bn﹣1=2n﹣1…②
①②两式相除得 ![]()
因为当n=1时,b1=3适合上式,所以 ![]() .
.
(2)
解:由已知 ![]() ,
,
得 ![]()
则Tn=c1+c2+c3+…+cn= ![]() ,
,
当n为偶数时, ![]()
= ![]()
= ![]() ,
,
当n为奇数时, ![]()
= ![]()
= ![]() .
.
综上:  .
.
【解析】(1)由题意和等差数列的前n项和公式求出公差,代入等差数列的通项公式化简求出an , 再化简b1b2b3…bn﹣1bn=an+2,可得当n≥2时b1b2b3…bn﹣1=2n﹣1,将两个式子相除求出bn;(2)由(1)化简cn=(﹣1)n ![]() ,再对n分奇数和偶数讨论,分别利用裂项相消法求出Tn , 最后要用分段函数的形式表示出来.
,再对n分奇数和偶数讨论,分别利用裂项相消法求出Tn , 最后要用分段函数的形式表示出来.
【考点精析】本题主要考查了等差数列的前n项和公式和数列的前n项和的相关知识点,需要掌握前n项和公式:![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系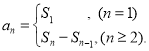 才能正确解答此题.
才能正确解答此题.

【题目】某公司的广告费支出x与销售额y(单位:万元)之间有下列对应数据
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
回归方程为 ![]() =bx+a,其中b=
=bx+a,其中b= 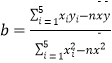 ,a=
,a= ![]() ﹣b
﹣b ![]() .
.
(1)画出散点图,并判断广告费与销售额是否具有相关关系;
(2)根据表中提供的数据,求出y与x的回归方程 ![]() =bx+a;
=bx+a;
(3)预测销售额为115万元时,大约需要多少万元广告费.