题目内容
【题目】已知椭圆![]() 和抛物线
和抛物线![]() 有公共焦点
有公共焦点![]() ,
, ![]() 的中心和
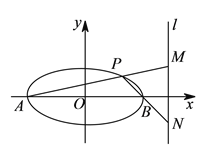
的中心和![]() 的顶点都在坐标原点,过点
的顶点都在坐标原点,过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 分别相交于
分别相交于![]() 两点(其中点
两点(其中点![]() 在第四象限内).
在第四象限内).
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若坐标原点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 在抛物线
在抛物线![]() 上,直线
上,直线![]() 与椭圆
与椭圆![]() 有公共点,求椭圆
有公共点,求椭圆![]() 的长轴长的最小值.
的长轴长的最小值.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:
(1)利用题意设直线![]() 的方程为
的方程为![]() .设出点的坐标可求得
.设出点的坐标可求得 ![]() .则直线
.则直线![]() 的方程为
的方程为![]() .
.
(2)由题意可得直线的斜率存在,设出直线方程,由对称性联立直线与抛物线的方程可得椭圆![]() 的长轴长的最小值为
的长轴长的最小值为![]()
试题解析:
解:(1)解法一:由题意得抛物线方程为![]() .
.
设直线![]() 的方程为
的方程为![]() .
.
令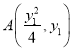 ,
, 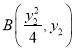 ,其中
,其中![]() . 由
. 由![]() ,得
,得![]() .
.
联立![]() ,可得
,可得![]() ,
,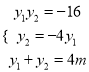 ,解得
,解得![]() ,
,![]() ,
,
![]()
![]() .
.
![]() 直线
直线![]() 的方程为
的方程为![]() .
.
(2)设![]() ,直线
,直线![]() ,
, ![]() 点
点![]() 在抛物线
在抛物线![]() 上,
上,
![]() 直线
直线![]() 的斜率存在,
的斜率存在, ![]()
![]() 关于直线
关于直线![]() 对称,所以
对称,所以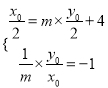 .解得
.解得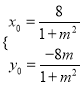 .
.
故![]() 代入抛物线
代入抛物线![]() ,可得
,可得![]() ,
, ![]() .
.
直线![]() 的方程为
的方程为![]() 或
或![]() .
.
设椭圆为![]() . 联立直线和椭圆,消去
. 联立直线和椭圆,消去![]() 整理得
整理得
![]()
![]()
![]()
![]()
![]() ,解得
,解得![]() .
.
则![]() ,即
,即![]() .
.![]() 椭圆
椭圆![]() 的长轴长的最小值为
的长轴长的最小值为![]()

练习册系列答案
相关题目
【题目】某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在![]() 内,发布成绩使用等级制各等级划分标准见下表,规定:
内,发布成绩使用等级制各等级划分标准见下表,规定: ![]() 、
、![]() 、
、![]() 三级为合格等级,
三级为合格等级, ![]() 为不合格等级.
为不合格等级.
百分制 |
|
|
|
|
等级 |
|
|
|
|
为了解该校高一年级学生身体素质情况,从中抽取了![]() 名学生的原始成绩作为样本进行统计,按照
名学生的原始成绩作为样本进行统计,按照![]() 的分组作出频率分布直方图如图
的分组作出频率分布直方图如图![]() 所示,样本中分数在
所示,样本中分数在![]() 分及以上的所有数据的茎叶图如图
分及以上的所有数据的茎叶图如图![]() 所示.
所示.
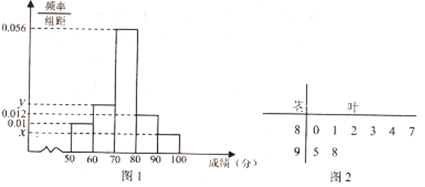
(1)求![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)根据样本估计总体的思想,以事件发生的频率作为相应事件发生的概率,若在该校高一学生任选![]() 人,求至少有
人,求至少有![]() 人成绩是合格等级的概率;
人成绩是合格等级的概率;
(3)在选取的样本中,从![]() 、
、![]() 两个等级的学生中随机抽取了
两个等级的学生中随机抽取了![]() 名学生进行调研,记
名学生进行调研,记![]() 表示所抽取的
表示所抽取的![]() 名学生中为
名学生中为![]() 等级的学生人数,求随机变量
等级的学生人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.