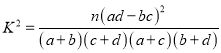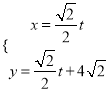题目内容
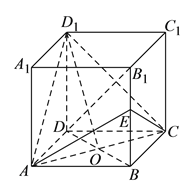
【题目】正方体![]() 的棱长为
的棱长为![]() ,
,![]() 是
是![]() 与
与![]() 的交点,
的交点,![]() 为
为![]() 的中点.
的中点.
(I)求证:直线![]() 平面
平面![]() .
.
(II)求证:![]() 平面
平面![]() .
.
(III)二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)见解析(3)![]()
【解析】试题分析:(1)先根据三角形中位线性质得![]() ,再根据线面平行判定定理得结论(2)由侧棱垂直底面得
,再根据线面平行判定定理得结论(2)由侧棱垂直底面得![]() ,由正方形性质得
,由正方形性质得![]() ,因此可由线面垂直判定定理得
,因此可由线面垂直判定定理得![]() 平面
平面![]() ,同理可得
,同理可得![]() ,从而有
,从而有![]() 面
面![]() .(3)利于空间向量求二面角:先建立空间直角坐标系,设立各点坐标,通过解方程组得各面法向量,根据向量数量积求法向量夹角,最后根据法向量夹角与二面角关系确定所求值
.(3)利于空间向量求二面角:先建立空间直角坐标系,设立各点坐标,通过解方程组得各面法向量,根据向量数量积求法向量夹角,最后根据法向量夹角与二面角关系确定所求值
(I)连接![]() ,在
,在![]() 中,
中,
∵![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
又∵![]() 面
面![]() ,
,
∴直线![]() 平面
平面![]() .
.
(II)在正方体![]() 中,
中,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() ,且
,且![]() ,
,
∴![]() ,
,
∴![]() ,
,
同理![]() ,
,
∵![]() ,
,
∴![]() 面
面![]() .
.
(III)以![]() 为原点,建立空间坐标系,
为原点,建立空间坐标系,
则![]() ,
,![]() ,
,
![]() ,
,![]() .
.
易知面![]() 的一法向量为
的一法向量为![]() ,
,
设面![]() 的一法向量为中
的一法向量为中![]() ,
,
∵![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∴![]() ,
,
设二面角![]() 为
为![]() ,
,
则![]()
![]() ,
,
故二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查得到如下列联表:
常喝 | 不常喝 | 合计 | |
肥胖 | 2 | ||
不肥胖 | 18 | ||
合计 | 30 |
已知在全部30人中随机抽取1人,抽到肥胖的学生的概率为![]() .
.
(1)请将上面的列表补充完整;
(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;
(3)4名调查人员随机分成两组,每组2人,一组负责问卷调查,另一组负责数据处理,求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: 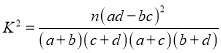 )
)