题目内容
【题目】已知几何体A﹣BCED的三视图如图所示，其中俯视图和侧视图都是腰长为4的等腰直角三角形，正视图为直角梯形，已知几何体A﹣BCED的体积为16． 
（1）求实数a的值；
（2）将直角三角形△ABD绕斜边AD旋转一周，求该旋转体的表面积．
【答案】
（1）解：由该几何体的三视图知AC⊥面BCED，且EC=BC=AC=4，BD=a，
体积V= 
=16，
解得a=2
（2）解：在RT△ABD中， 
，BD=2，AD=6，
过B作AD的垂线BH，垂足为H，得 
，
该旋转体由两个同底的圆锥构成，圆锥底面半径为 ，
所以圆锥底面周长为 
，两个圆锥的母线长分别为 
和2，
故该旋转体的表面积为 
【解析】（1）由该几何体的三视图知AC⊥面BCED，且EC=BC=AC=4，BD=a，利用几何体A﹣BCED的体积为16，求实数a的值；（2）过B作AD的垂线BH，垂足为H，得 ，求出圆锥底面周长为 ，两个圆锥的母线长分别为 和2，即可求该旋转体的表面积．
【考点精析】解答此题的关键在于理解由三视图求面积、体积的相关知识，掌握求体积的关键是求出底面积和高；求全面积的关键是求出各个侧面的面积，以及对旋转体（圆柱、圆锥、圆台）的理解，了解常见的旋转体有：圆柱、圆锥、圆台、球．
【题目】某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在
内,发布成绩使用等级制各等级划分标准见下表,规定： 
、
、
三级为合格等级, 
为不合格等级.
百分制 |
|
|
|
|
等级 |
|
|
|
|
为了解该校高一年级学生身体素质情况,从中抽取了
名学生的原始成绩作为样本进行统计,按照
的分组作出频率分布直方图如图
所示,样本中分数在
分及以上的所有数据的茎叶图如图
所示.
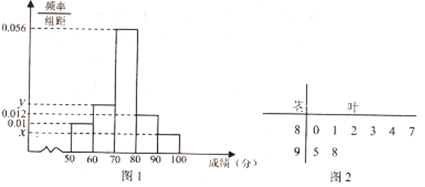
（1）求
和频率分布直方图中的
的值；
（2）根据样本估计总体的思想，以事件发生的频率作为相应事件发生的概率，若在该校高一学生任选
人,求至少有
人成绩是合格等级的概率；
（3）在选取的样本中,从
、
两个等级的学生中随机抽取了
名学生进行调研,记
表示所抽取的
名学生中为
等级的学生人数,求随机变量
的分布列及数学期望.
