题目内容
已知函数 .
.
(1)从区间 内任取一个实数
内任取一个实数 ,设事件
,设事件 ={函数
={函数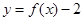 在区间
在区间 上有两个不同的零点},求事件
上有两个不同的零点},求事件 发生的概率;
发生的概率;
(2)若连续掷两次骰子(骰子六个面上标注的点数分别为 )得到的点数分别为
)得到的点数分别为 和
和 ,记事件
,记事件 {
{ 在
在 恒成立},求事件
恒成立},求事件 发生的概率.
发生的概率.
(1)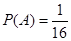 ;(2)
;(2)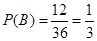 .
.
解析试题分析:(1)根据函数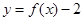 在区间
在区间 上有两个不同的零点,
上有两个不同的零点,
得知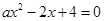 有两个不同的正根
有两个不同的正根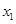 和
和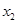 ,
,
由不等式组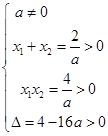
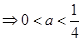 ,利用几何概型得解.
,利用几何概型得解.
(2)应用基本不等式得到 ,
,
由于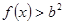 在
在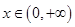 恒成立,得到
恒成立,得到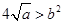 ;
;
讨论当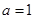 ,
,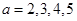 ,
,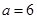 的情况,
的情况,
得到满足条件的基本事件个数,而基本事件总数为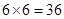 , 故应用古典概型概率的计算公式即得解.
, 故应用古典概型概率的计算公式即得解.
试题解析:(1)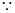 函数
函数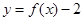 在区间
在区间 上有两个不同的零点,
上有两个不同的零点,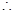
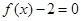 ,即
,即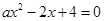 有两个不同的正根
有两个不同的正根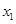 和
和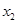
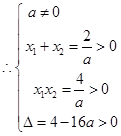
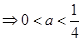 4分
4分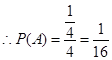 6分
6分
(2)由已知: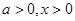 ,所以
,所以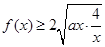 ,即
,即
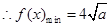 ,
, 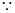
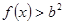 在
在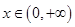 恒成立
恒成立 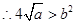
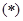 8分
8分
当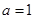 时,
时,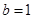 适合
适合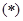 ;
;
当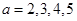 时,
时,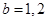 均适合
均适合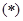 ;
;
当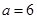 时,
时,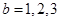 均适合
均适合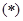 ;
;
满足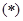 的基本事件个数为
的基本事件个数为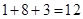 . 10分
. 10分
而基本事件总数为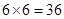 , 11分
, 11分 . 12分
. 12分
考点:古典概型,几何概型,一元二次方程根的分别,基本不等式的应用,不等式恒成立问题.

对有 个元素的总体
个元素的总体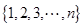 进行抽样,先将总体分成两个子总体
进行抽样,先将总体分成两个子总体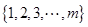 和
和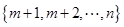 (
(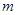 是给定的正整数,且
是给定的正整数,且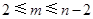 ),再从每个子总体中各随机抽取
),再从每个子总体中各随机抽取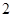 个元素组成样本.用
个元素组成样本.用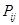 表示元素
表示元素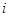 和
和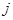 同时出现在样本中的概率.
同时出现在样本中的概率.
(1)求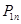 的表达式(用
的表达式(用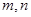 表示);
表示);
(2)求所有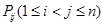 的和.
的和.
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
| 测试指标 |  | 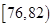 |  |  | 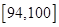 |
| 元件A | 8 | 12 | 40 | 32] | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
(2)生产一件元件A,若是正品可盈利50元,若是次品则亏损10元;生产一件元件B,若是正品可盈利100元,若是次品则亏损20元,在(1)的前提下;
(i)求生产5件元件B所获得的利润不少于300元的概率;
(ii)记X为生产1件元件A和1件元件B所得的总利润,求随机变量X的分布列和数学期望.
 为甲、乙、丙这三个学生选修数学史这门课的人数,求
为甲、乙、丙这三个学生选修数学史这门课的人数,求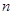 个黑球(
个黑球(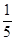 ,求
,求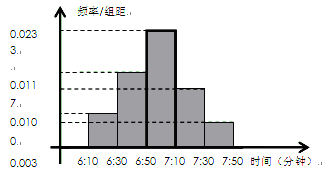
 和中位数
和中位数 (精确到整数分钟);
(精确到整数分钟); 在上午
在上午 之间,而送报人每天在
之间,而送报人每天在 )的概率.
)的概率. 、a、a(0<a<1),三人各射击一次,击中目标的次数记为ξ.
、a、a(0<a<1),三人各射击一次,击中目标的次数记为ξ.