题目内容
已知函数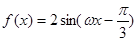 (
(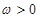 )的最小正周期为
)的最小正周期为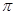 .
.
(1)求函数 的单调增区间;
的单调增区间;
(2)将函数 的图像向左平移
的图像向左平移 个单位,再向上平移
个单位,再向上平移 个单位,得到函数
个单位,得到函数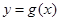 的图像.求
的图像.求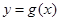 在区间
在区间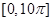 上零点的个数.
上零点的个数.
(1)函数 的单调增区间
的单调增区间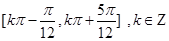 ;(2)
;(2) 在
在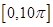 上有
上有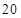 个零点.
个零点.
解析试题分析:(1)先由三角函数的周期计算公式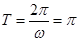 得到
得到 ,从而可确定
,从而可确定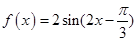 ,将
,将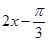 当成一个整体,由正弦函数的性质得到
当成一个整体,由正弦函数的性质得到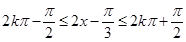 ,解出
,解出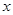 的范围,写成区间即是所求函数的单调递增区间;(2)将函数
的范围,写成区间即是所求函数的单调递增区间;(2)将函数 的图像向左平移
的图像向左平移 个单位,再向上平移1个单位,得到
个单位,再向上平移1个单位,得到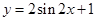 的图像,即
的图像,即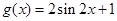 ,由正弦函数的图像与性质得到该函数在一个周期内函数零点的个数,而
,由正弦函数的图像与性质得到该函数在一个周期内函数零点的个数,而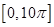 恰为
恰为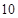 个周期,从而可得
个周期,从而可得 在
在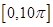 上零点的个数.
上零点的个数.
试题解析:(1)由周期为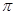 ,得
,得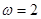 ,得
,得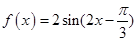
由正弦函数的单调增区间得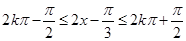 ,得
,得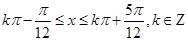
所以函数 的单调增区间
的单调增区间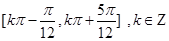
(2)将函数 的图像向左平移
的图像向左平移 个单位,再向上平移1个单位
个单位,再向上平移1个单位
得到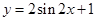 的图像,所以
的图像,所以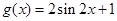
令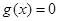 ,得
,得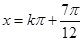 或
或
所以函数在每个周期上恰有两个零点, 恰为
恰为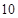 个周期,故
个周期,故 在
在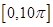 上有
上有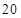 个零点.
个零点.
考点:1.三角函数的图像与性质;2.函数的零点.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
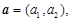
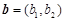 ,定义一种向量积
,定义一种向量积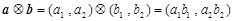 .
.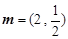 ,
,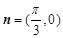 ,点
,点 为
为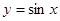 的图象上的动点,点
的图象上的动点,点
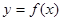 的图象上的动点,且满足
的图象上的动点,且满足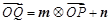 (其中
(其中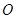 为坐标原点).
为坐标原点).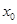 表示
表示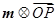 ;
; 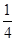 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数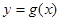 的图象.设函数
的图象.设函数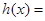
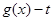
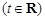 ,试讨论函数
,试讨论函数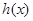 在区间
在区间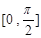 内的零点个数.
内的零点个数.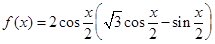 .
.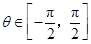 ,且
,且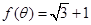 ,求
,求 的值;
的值;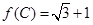 ,且△ABC的面积为
,且△ABC的面积为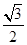 ,求sinA+sinB的值.
,求sinA+sinB的值. 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为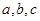 ,已知向量
,已知向量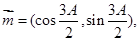
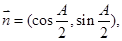 且满足
且满足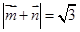 .
. 试判断
试判断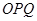 是半径为
是半径为 ,圆心角为
,圆心角为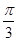 的扇形,
的扇形,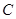 是扇形弧上的动点,
是扇形弧上的动点,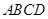 是扇形的内接矩形.记
是扇形的内接矩形.记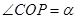 ,求当角
,求当角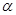 取何值时,矩形
取何值时,矩形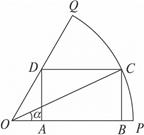
 .
. 的最小正周期及对称轴方程;
的最小正周期及对称轴方程;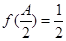 ,bc=6,求a的最小值.
,bc=6,求a的最小值. ,函数
,函数 .
. ,x为某三角形的内角,求
,x为某三角形的内角,求 时x的值;
时x的值; ,当函数
,当函数 取最大值时,求cos2x的值.
取最大值时,求cos2x的值.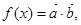 其中向量
其中向量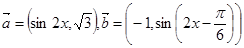 ,
,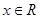 .
. 的最小值,并求使
的最小值,并求使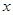 的集合;
的集合;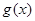 的图象关于
的图象关于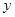 轴对称?
轴对称?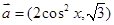 ,
,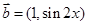 ,函数
,函数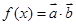 .
. 的最小正周期;
的最小正周期;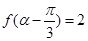 ,
,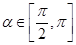 ,求
,求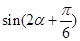 的值.
的值.