题目内容
已知向量 ,函数
,函数 .
.
⑴设 ,x为某三角形的内角,求
,x为某三角形的内角,求 时x的值;
时x的值;
⑵设 ,当函数
,当函数 取最大值时,求cos2x的值.
取最大值时,求cos2x的值.
⑴ ;⑵
;⑵ .
.
解析试题分析:首先由数量积公式得 .⑴将
.⑴将 ,
, 代入
代入 可得
可得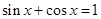 ,将化一得
,将化一得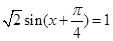 ,即
,即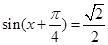 ,
,
又因为 为三角形的内角,所以
为三角形的内角,所以 ;⑵将
;⑵将 代入
代入 可得
可得 ,其中
,其中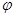 为锐角,且
为锐角,且 ,当且仅当
,当且仅当 时,函数
时,函数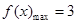 .此时
.此时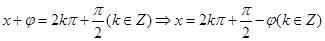 ,所以
,所以 ,则
,则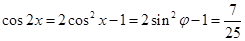 .
.
试题解析:由题可知, ,
,
⑴当 时,
时,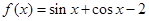 ,
,
∵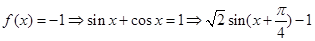
∴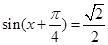 ,
,
∵ 为三角形的内角,∴
为三角形的内角,∴ . .5分
. .5分
⑵当 时,
时, ,其中
,其中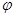 为锐角,且
为锐角,且 ,
,
当且仅当 时,函数
时,函数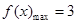 .
.
此时
∴ ,则
,则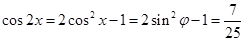 12分
12分
考点:向量及三角函数.

练习册系列答案
相关题目
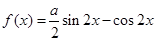 的图象过点
的图象过点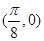 .
.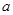 的值;
的值; 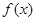 的最小正周期及最大值.
的最小正周期及最大值.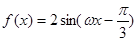 (
(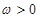 )的最小正周期为
)的最小正周期为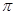 .
. 的单调增区间;
的单调增区间; 个单位,再向上平移
个单位,再向上平移 个单位,得到函数
个单位,得到函数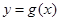 的图像.求
的图像.求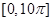 上零点的个数.
上零点的个数. =
= ,那么sin
,那么sin 的值为 ,cos2
的值为 ,cos2 .
. 的最小正周期;
的最小正周期; ,求cosθ的值.
,求cosθ的值.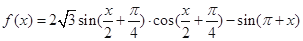 .
. 的最小正周期.
的最小正周期.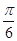 个单位,得到函数
个单位,得到函数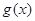 的图象,求函数
的图象,求函数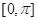 上的值域.
上的值域. cos4x.
cos4x. ,π),且f(α)=
,π),且f(α)=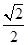 ,求α的值.
,求α的值.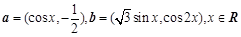 , 设函数
, 设函数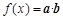 .
.  上的最大值和最小值.
上的最大值和最小值.