题目内容
已知函数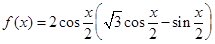 .
.
(1)设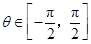 ,且
,且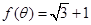 ,求
,求 的值;
的值;
(2)在△ABC中,AB=1,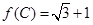 ,且△ABC的面积为
,且△ABC的面积为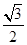 ,求sinA+sinB的值.
,求sinA+sinB的值.
(1)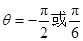 ,(2)
,(2)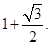
解析试题分析:(1)研究三角函数性质,首先将三角函数化为基本三角函数形式,即: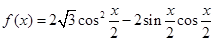 =
=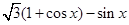 =
=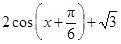 .再由
.再由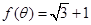 得
得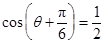 于是
于是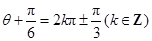 ,因为
,因为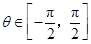 ,所以
,所以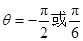 .(2)解三角形,基本方法利用正余弦定理进行边角转化. 因为△ABC的面积为,所以
.(2)解三角形,基本方法利用正余弦定理进行边角转化. 因为△ABC的面积为,所以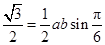 ,于是
,于是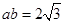 .因为
.因为 ,由(1)知
,由(1)知 .由余弦定理得
.由余弦定理得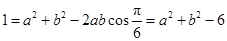 ,所以
,所以 .可得
.可得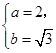 或
或 由正弦定理得
由正弦定理得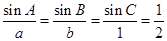 ,所以
,所以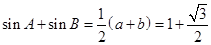 .
.
【解】(1) =
=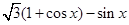 =
=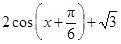 .
.
由 ,得
,得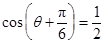 ,
,
于是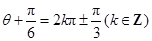 ,因为
,因为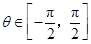 ,所以
,所以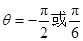 .
. 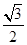
(2)因为 ,由(1)知
,由(1)知 .
.
因为△ABC的面积为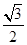 ,所以
,所以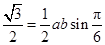 ,于是
,于是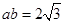 . ①
. ①
在△ABC中,设内角A、B的对边分别是a,b.
由余弦定理得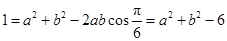 ,所以
,所以 . ②
. ②
由①②可得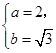 或
或 于是
于是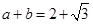 .
.
由正弦定理得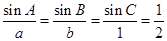 ,
,
所以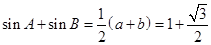 .
.
考点:三角函数性质,正余弦定理

练习册系列答案
相关题目
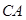 、
、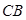 的夹角为
的夹角为 (即
(即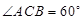 ),现有可供建造第三面围墙的材料
),现有可供建造第三面围墙的材料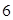 米(两面墙的长均大于
米(两面墙的长均大于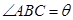 ,问当
,问当 为多少时,所建造的三角形露天仓库的面积最大,并求出最大值?
为多少时,所建造的三角形露天仓库的面积最大,并求出最大值? 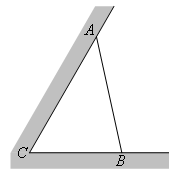
 ,求
,求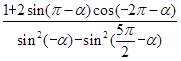 的值.
的值. 的部分图象,如图所示.
的部分图象,如图所示.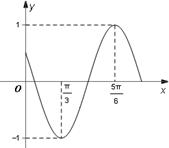
 在
在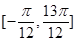 有两个不同的实根,求
有两个不同的实根,求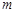 的取值范围.
的取值范围.
 的最小正周期;
的最小正周期; 时,求函数f(x)的单调区间。
时,求函数f(x)的单调区间。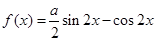 的图象过点
的图象过点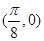 .
.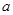 的值;
的值; 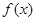 的最小正周期及最大值.
的最小正周期及最大值.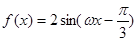 (
(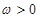 )的最小正周期为
)的最小正周期为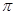 .
. 的单调增区间;
的单调增区间; 个单位,再向上平移
个单位,再向上平移 个单位,得到函数
个单位,得到函数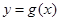 的图像.求
的图像.求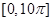 上零点的个数.
上零点的个数.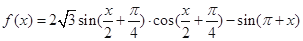 .
. 的最小正周期.
的最小正周期.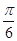 个单位,得到函数
个单位,得到函数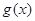 的图象,求函数
的图象,求函数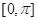 上的值域.
上的值域.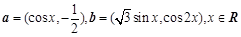 , 设函数
, 设函数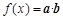 .
.  上的最大值和最小值.
上的最大值和最小值.