题目内容
4.在一台车床上生产某种零件,此零件的月产量与零件的市场价格具有随机性,且互不影响,其具体情况如表:表1:零件某年的每月产量(个/月)
| 月份 | 第一季度 | 第二季度 | 第三季度 | 第四季度 | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 产量 | 500 | 400 | 625 | 625 | 500 | 500 | 500 | 500 | 500 | 400 | 400 | 625 |
| 零件市场价格 | 8 | 10 |
| 概率 | 0.4 | 0.6 |
(Ⅱ) 随机抽取该种零件的一个月的月产量记为X,求X的分布列;
(Ⅲ)随机抽取该种零件的一个月的月产量,设Y表示该种零件的月产值,求Y的分布列及期望.
分析 (I)运用给出的数据的差异可判断得出不稳定问题,可判断方差的大小问题.
(II) X取值为X=400,500,625.运用表格数据可得出P(X=400)=0.25;P(X=500)=0.5;P(X=625)=0.25.
可列出分布列.
(III)确定随机变量Y的所有可能取值为Y=3200,4000,5000,6250.
运用表的概率知识和则P(X=400)=0.25;P(X=500)=0.5;P(X=625)=0.25.
求解得出P(Y=3200)=0.1,(Y=4000)=0.35,P(Y=5000)=0.4,P(Y=6250)=0.15
列出分布列,求解数学期望.
解答 解:(I) 第四季度的月产量方差最大.
(II) X取值为X=400,500,625.
则P(X=400)=0.25;P(X=500)=0.5;P(X=625)=0.25.
所以随机变量X的分布列为
| X | 400 | 500 | 625 |
| P | 0.25 | 0.5 | 0.25 |
所以随机变量Y的所有可能取值为Y=3200,4000,5000,6250.
所以P(Y=3200)=0.4×0.25=0.1,
P(Y=4000)=0.6×0.25+0.4×0.5=0.35,
P(Y=5000)=0.6×0.5+0.4×0.25=0.4,
P(Y=6250)=0.6×0.25=0.15
所以随机变量Y的分布列为
| Y | 3200 | 4000 | 5000 | 6250 |
| P | 0.1 | 0.35 | 0.4 | 0.15 |
点评 题综合考查了概率在实际问题中的应用,关键是准确求解概率,判断概率的类型,准确求解即可,熟练运用公式计算求解,仔细阅读题意.

练习册系列答案
相关题目
19.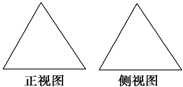 如图是两个全等的正三角形,给出下列三个命题:①存在四棱锥,其正视图、侧视图如图;②存在三棱锥,其正视图、侧视图如图;③存在圆锥,其正视图、侧视图如图.其中所有真命题的序号是( )
如图是两个全等的正三角形,给出下列三个命题:①存在四棱锥,其正视图、侧视图如图;②存在三棱锥,其正视图、侧视图如图;③存在圆锥,其正视图、侧视图如图.其中所有真命题的序号是( )
 如图是两个全等的正三角形,给出下列三个命题:①存在四棱锥,其正视图、侧视图如图;②存在三棱锥,其正视图、侧视图如图;③存在圆锥,其正视图、侧视图如图.其中所有真命题的序号是( )
如图是两个全等的正三角形,给出下列三个命题:①存在四棱锥,其正视图、侧视图如图;②存在三棱锥,其正视图、侧视图如图;③存在圆锥,其正视图、侧视图如图.其中所有真命题的序号是( )| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
9.设i为虚数单位,复数z=(1+i)2+2,则z的共轭复数为( )
| A. | -2i | B. | 2i | C. | 2-2i | D. | 2+2i |
14.已知m,n是两条不同的直线,α、β是两个不同的平面,则下列命题中正确的是( )
| A. | 若α⊥β,m∥α,则m⊥β | B. | 若m∥α,n∥m,则n∥α | ||
| C. | 若m∥α,n∥β,且m∥n,则α∥β | D. | 若m⊥β,m∥α,则α⊥β |