题目内容
12.设实数x,y满足$\left\{{\begin{array}{l}{x≥1\;\;\;\;\;\;}\\{y≥x-1\;}\\{x+y≤3\;}\end{array}}\right.$,则动点P(x,y)所形成区域的面积为1,z=x2+y2的取值范围是[1,5].分析 先画出满足条件的平面区域,求出A,B,C的坐标,从而求出三角形的面积,再根据z=x2+y2的几何意义,求出其范围即可.
解答 解:画出满足条件的平面区域,如图示: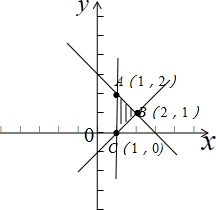 ,
,
△ABC为平面区域的面积,
∴S△ABC=$\frac{1}{2}$×2×1=1,
而z=x2+y2表示平面区域内的点到原点的距离的平方,
由图象得:A或B到原点的距离最大,C到原点的距离最小,
∴d最大值=5,d最小值=1,
故答案为:1,[1,5].
点评 本题考察了简单的线性规划问题,考察z=x2+y2的几何意义,本题是一道中档题.

练习册系列答案
相关题目
3.5名学生和2名老师排成一排照相,2名老师不在两边且不相邻的概率为( )
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{7}$ |
7.函数y=(2x-1)ex的图象是( )
| A. |  | B. |  | C. |  | D. |  |
2.定义在R上的奇函数y=f(x)满足当x>0时,f(x)=xlnx,则当x<0时,f′(x)=( )
| A. | -ln(-x)+1 | B. | ln(-x)+1 | C. | -ln(-x)-1 | D. | ln(-x)-1 |