题目内容
4.函数y=|sinx+$\frac{1}{2}$|的最小正周期是2π,在(0,2π)内的单调递减区间是($\frac{π}{2}$,π)、($\frac{3π}{2}$,2π).分析 由条件结合函数y=|sinx+$\frac{1}{2}$|的图象特征,可得结论.
解答  解:由函数y=|sinx+$\frac{1}{2}$|的图象特征可得函数y=|sinx+$\frac{1}{2}$|的最小正周期是就是函数y=sinx的最小正周期是2π,
解:由函数y=|sinx+$\frac{1}{2}$|的图象特征可得函数y=|sinx+$\frac{1}{2}$|的最小正周期是就是函数y=sinx的最小正周期是2π,
如图所示:
故在(0,2π)内的单调递减区间是($\frac{π}{2}$,π)、($\frac{3π}{2}$,2π),
故答案为:2π;($\frac{π}{2}$,π)、($\frac{3π}{2}$,2π).
点评 本题主要考查正弦函数的图象特征,体现了转化、数形结合的数学思想,属于基础题.

练习册系列答案
相关题目
14.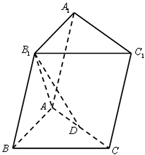 如图,在三棱柱ABC-A1B1C1中,B1B=B1A=BA=BC=2,∠B1BC=90°,D为AC的中点,AB⊥B1D.
如图,在三棱柱ABC-A1B1C1中,B1B=B1A=BA=BC=2,∠B1BC=90°,D为AC的中点,AB⊥B1D.
(Ⅰ)求证:平面ABC⊥平面ABB1A1;
(Ⅱ)求B到平面AB1D的距离.
 如图,在三棱柱ABC-A1B1C1中,B1B=B1A=BA=BC=2,∠B1BC=90°,D为AC的中点,AB⊥B1D.
如图,在三棱柱ABC-A1B1C1中,B1B=B1A=BA=BC=2,∠B1BC=90°,D为AC的中点,AB⊥B1D.(Ⅰ)求证:平面ABC⊥平面ABB1A1;
(Ⅱ)求B到平面AB1D的距离.
15.将函数y=sin(2x-ϕ)(0<ϕ<π)的图象沿x轴向左平移$\frac{π}{6}$个单位后得到的图象关于原点对称,则ϕ的值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
19.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一个交点与抛物线y2=8x的焦点重合,且双曲线的离心率等于$\sqrt{2}$,则该双曲线的方程为( )
| A. | x2-y2=4 | B. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{y}^{2}}{5}$-$\frac{{x}^{2}}{4}$=1 | D. | x2-y2=2 |
9.钝角△ABC的三个内角A、B、C的对边分别为a、b、c,A=$\frac{π}{4}$,sin2B+cos22C=1.
(1)求角B,C;
(2)若a2+c2=b+$\sqrt{3}$ac+2,求a.
(1)求角B,C;
(2)若a2+c2=b+$\sqrt{3}$ac+2,求a.
16.已知函数f(x)=x2-2x+4,数列{an}是公差为d的等差数列,若a1=f(d-1),a3=f(d+1),则{an}的通项公式为( )
| A. | 2n-2 | B. | 2n+1 | C. | 2n+3 | D. | n+2 |