题目内容
3．5名学生和2名老师排成一排照相，2名老师不在两边且不相邻的概率为（ ）| A． | $\frac{1}{7}$ | B． | $\frac{2}{7}$ | C． | $\frac{4}{7}$ | D． | $\frac{5}{7}$ |
分析 由排列组合的知识可得总的排法和2名老师不在两边且不相邻的排法，由概率公式可得．
解答 解：7人排队共有${A}_{7}^{7}$种方法，
其中2名老师不在两边且不相邻，
可先排5名学生共${A}_{5}^{5}$种方法，再从产生的中间4个空位任选2个排列2位老师
共${A}_{4}^{2}$种方法，由分步计数原理可得共${A}_{5}^{5}$${A}_{4}^{2}$种方法，
故所求概率P=$\frac{{A}_{5}^{5}•{A}_{4}^{2}}{{A}_{7}^{7}}$=$\frac{2}{7}$
故选：B．
点评 本题考查排列组合在古典概型中的应用，属基础题．
练习册系列答案
相关题目
，则函数
与函数
的图象交点的个数为（ ）
14．
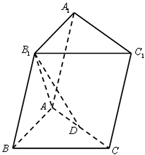如图，在三棱柱ABC-A1B1C1中，B1B=B1A=BA=BC=2，∠B1BC=90°，D为AC的中点，AB⊥B1D．
（Ⅰ）求证：平面ABC⊥平面ABB1A1；
（Ⅱ）求B到平面AB1D的距离．
如图，在三棱柱ABC-A1B1C1中，B1B=B1A=BA=BC=2，∠B1BC=90°，D为AC的中点，AB⊥B1D．（Ⅰ）求证：平面ABC⊥平面ABB1A1；
（Ⅱ）求B到平面AB1D的距离．
18．已知x，y满足$\left\{\begin{array}{l}x-y≥0\\ x+y≤4\\ y≥1\end{array}$，且z=$\frac{1}{2}$x+y的最大值是M，最小值是m，若 Ma+mb=3（a，b均为正实数），则$\frac{2}{a}$+$\frac{1}{b}$的最小值为（ ）
| A． | 4 | B． | $\frac{9}{2}$ | C． | 8 | D． | 9 |
8．如图所示，正弦曲线y=sinx，余弦曲线y=cosx与两直线x=0，x=π所围成的阴影部分的面积为（ ）
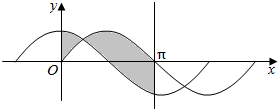
| A． | 1 | B． | $\sqrt{2}$ | C． | 2 | D． | 2$\sqrt{2}$ |
15．将函数y=sin（2x-ϕ）（0＜ϕ＜π）的图象沿x轴向左平移$\frac{π}{6}$个单位后得到的图象关于原点对称，则ϕ的值为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{2π}{3}$ | D． | $\frac{5π}{6}$ |