题目内容
7．函数y=（2x-1）ex的图象是（ ）| A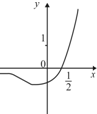． |  | B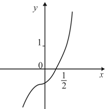． |  | C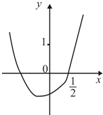． |  | D． |  |
分析 先通过函数的零点排除C，D，再根据x的变化趋势和y的关系排除B，问题得以解决．
解答 解：令y=（2x-1）ex=0，解得x=$\frac{1}{2}$，函数有唯一的零点，故排除C，D，
当x→-∞时，ex→0，所以y→0，故排除B，
故选：A．
点评 本小题主要考查函数的性质对函数图象的影响，并通过对函数的性质来判断函数的图象等问题．
练习册系列答案
相关题目
18．已知x，y满足$\left\{\begin{array}{l}x-y≥0\\ x+y≤4\\ y≥1\end{array}$，且z=$\frac{1}{2}$x+y的最大值是M，最小值是m，若 Ma+mb=3（a，b均为正实数），则$\frac{2}{a}$+$\frac{1}{b}$的最小值为（ ）
| A． | 4 | B． | $\frac{9}{2}$ | C． | 8 | D． | 9 |
15．将函数y=sin（2x-ϕ）（0＜ϕ＜π）的图象沿x轴向左平移$\frac{π}{6}$个单位后得到的图象关于原点对称，则ϕ的值为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{2π}{3}$ | D． | $\frac{5π}{6}$ |
19．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一个交点与抛物线y2=8x的焦点重合，且双曲线的离心率等于$\sqrt{2}$，则该双曲线的方程为（ ）
| A． | x2-y2=4 | B． | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{4}$=1 | C． | $\frac{{y}^{2}}{5}$-$\frac{{x}^{2}}{4}$=1 | D． | x2-y2=2 |
16．已知函数f（x）=x2-2x+4，数列{an}是公差为d的等差数列，若a1=f（d-1），a3=f（d+1），则{an}的通项公式为（ ）
| A． | 2n-2 | B． | 2n+1 | C． | 2n+3 | D． | n+2 |
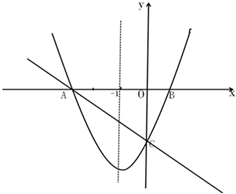如图，在直角坐标系xOy中，一次函数y=-$\frac{2}{3}$x+m（m为常数）的图象与x轴交于A（-3，0），与y轴交于点C．以直线x=-1为对称轴的抛物线y=ax2+bx+c（a，b，c为常数，且a＞0）经过A、C两点，与x轴正半轴交于点B．