题目内容
(本小题满分12分)
已知点 ,
, 是平面上一动点,且满足
是平面上一动点,且满足 ,
,
(1)求点 的轨迹
的轨迹 对应的方程;
对应的方程;
(2)已知点 在曲线
在曲线 上,过点
上,过点 作曲线
作曲线 的两条弦
的两条弦 ,且
,且 的斜率为
的斜率为 满足
满足 ,试判断动直线
,试判断动直线 是否过定点,并证明你的结论.
是否过定点,并证明你的结论.
已知点
 ,
, 是平面上一动点,且满足
是平面上一动点,且满足 ,
,(1)求点
 的轨迹
的轨迹 对应的方程;
对应的方程;(2)已知点
 在曲线
在曲线 上,过点
上,过点 作曲线
作曲线 的两条弦
的两条弦 ,且
,且 的斜率为
的斜率为 满足
满足 ,试判断动直线
,试判断动直线 是否过定点,并证明你的结论.
是否过定点,并证明你的结论. (1)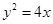 即为
即为 对应的方程;(2)直线
对应的方程;(2)直线 恒过定点
恒过定点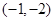 .
.
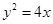 即为
即为 对应的方程;(2)直线
对应的方程;(2)直线 恒过定点
恒过定点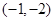 .
.第一问是平面向量与解析几何得结合,体现了向量运算的工具作用。熟练向量的运算对于解决这类问题很有帮助。第二问考查直线与圆锥曲线的位置关系,解题的思路一般是将直线方程代入曲线方程消去一个未知数,然后利用韦达定理处理。
解:(1)由 可知
可知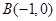 …………………………1分
…………………………1分
设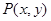 ,则
,则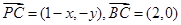 ,
,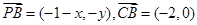 …………2分
…………2分
代入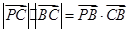 得:
得: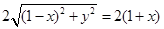
化简得: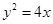 即为
即为 对应的方程, …………………………5分
对应的方程, …………………………5分
(2)将 代入
代入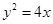 得
得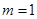 ∴
∴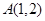 …………………………6分
…………………………6分
设直线 的方程为:
的方程为: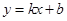
代入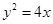 消
消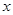 得:
得: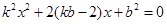 …………………………7分
…………………………7分
记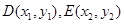
则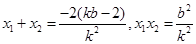 …………………………8分
…………………………8分
∵ ∴
∴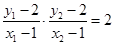 且
且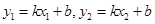
∴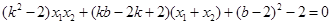
∴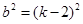
∴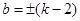 …………………………10分
…………………………10分
当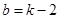 时代入
时代入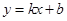 得:
得: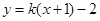 过定点
过定点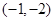
当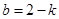 时代入
时代入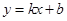 得:
得: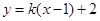 过
过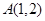 ,不合题意,舍去.
,不合题意,舍去.
综上可知直线 恒过定点
恒过定点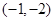 .…………………………12分
.…………………………12分
解:(1)由
 可知
可知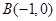 …………………………1分
…………………………1分设
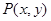 ,则
,则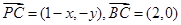 ,
,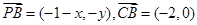 …………2分
…………2分代入
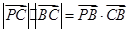 得:
得: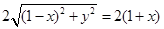
化简得:
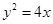 即为
即为 对应的方程, …………………………5分
对应的方程, …………………………5分(2)将
 代入
代入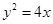 得
得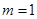 ∴
∴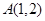 …………………………6分
…………………………6分设直线
 的方程为:
的方程为: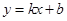
代入
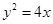 消
消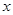 得:
得: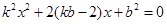 …………………………7分
…………………………7分记
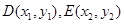
则
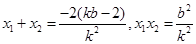 …………………………8分
…………………………8分∵
 ∴
∴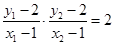 且
且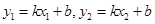
∴
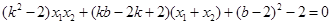
∴
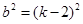
∴
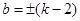 …………………………10分
…………………………10分当
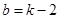 时代入
时代入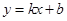 得:
得: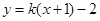 过定点
过定点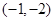
当
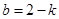 时代入
时代入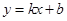 得:
得: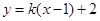 过
过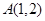 ,不合题意,舍去.
,不合题意,舍去.综上可知直线
 恒过定点
恒过定点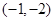 .…………………………12分
.…………………………12分
练习册系列答案
相关题目
 ,则它的一个焦点到一条渐进线的距离是( )
,则它的一个焦点到一条渐进线的距离是( ) D. 12
D. 12 上的任意一点到它两个焦点
上的任意一点到它两个焦点 的距离之和为
的距离之和为 ,且它的焦距为2.
,且它的焦距为2. 的方程;
的方程; 与椭圆
与椭圆 ,且线段
,且线段 的中点
的中点 不在圆
不在圆 内,求实数
内,求实数 的取值范围.
的取值范围.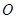 为圆心,
为圆心,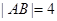 为直径的半圆
为直径的半圆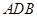 中,
中,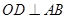 ,
,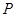 是半圆弧上一点,
是半圆弧上一点,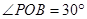 ,曲线
,曲线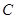 是满足
是满足 为定值的动点
为定值的动点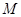 的轨迹,且曲线
的轨迹,且曲线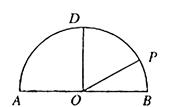
 的直线l与曲线
的直线l与曲线 、
、
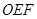 的面积不小于
的面积不小于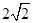 ,求直线
,求直线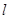 斜率的取值范围.
斜率的取值范围.  ,直线AM,BM相交于点M,且它们的斜率之和是2,则点M的轨迹方程是( )
,直线AM,BM相交于点M,且它们的斜率之和是2,则点M的轨迹方程是( )



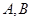 两城市作为龙头带动周边城市的发展,决定在
两城市作为龙头带动周边城市的发展,决定在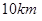 为一个单位距离,
为一个单位距离, 个单位距离,设城际轻轨所在的曲线为
个单位距离,设城际轻轨所在的曲线为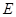 ,使轻轨
,使轻轨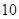 个单位距离,
个单位距离,
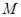 与一个收费站
与一个收费站 ,使
,使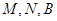 三点在一条直线上,并且
三点在一条直线上,并且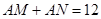 个单位距离,求
个单位距离,求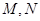 之间的距离有多少个单位距离?
之间的距离有多少个单位距离?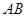 所在直线成
所在直线成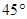 的笔直公路
的笔直公路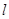 ,直线
,直线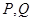 两点,求四边形
两点,求四边形 的面积的最大值.
的面积的最大值. 与
与 轴的正半轴相交于
轴的正半轴相交于 点,
点, 两点在圆
两点在圆 上,
上, 在第一象限,
在第一象限, 在第二象限,
在第二象限, ,则劣弧
,则劣弧 所对圆 心角的余弦值为( )
所对圆 心角的余弦值为( )



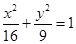 的左、右焦点分别为
的左、右焦点分别为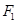 、
、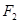 , 过焦点F1的直线交椭圆于
, 过焦点F1的直线交椭圆于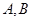 两点,若
两点,若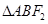 的内切圆的面积为
的内切圆的面积为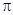 ,
,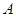 ,
,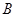 两点的坐标分别为
两点的坐标分别为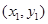 和
和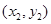 ,则
,则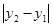 的值为___________。
的值为___________。 与双曲线
与双曲线 有相同的焦点
有相同的焦点 ,
, 是两曲线的一个交点,则
是两曲线的一个交点,则 等于 ( )
等于 ( ) 


