题目内容
椭圆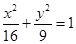 的左、右焦点分别为
的左、右焦点分别为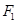 、
、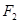 , 过焦点F1的直线交椭圆于
, 过焦点F1的直线交椭圆于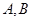 两点,若
两点,若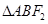 的内切圆的面积为
的内切圆的面积为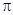 ,
,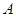 ,
,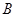 两点的坐标分别为
两点的坐标分别为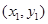 和
和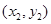 ,则
,则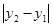 的值为___________。
的值为___________。
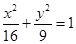 的左、右焦点分别为
的左、右焦点分别为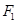 、
、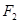 , 过焦点F1的直线交椭圆于
, 过焦点F1的直线交椭圆于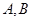 两点,若
两点,若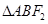 的内切圆的面积为
的内切圆的面积为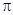 ,
,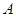 ,
,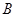 两点的坐标分别为
两点的坐标分别为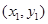 和
和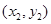 ,则
,则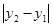 的值为___________。
的值为___________。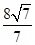
解:椭圆:x2/ 16 +y2/ 9 =1,a=4,b=3,∴c=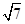 7 ,
7 ,
左、右焦点F1(-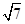 ,0)、F2(
,0)、F2( 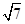 ,0),
,0),
△ABF2的内切圆面积为π,则内切圆的半径为r=1,
而△ABF2的面积=△AF1F2的面积+△BF1F2的面积="1" /2 ×|y1|×|F1F2|+1/ 2 ×|y2|×|F1F2|="1" /2 ×(|y1|+|y2|)×|F1F2|=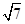 |y2-y1|(A、B在x轴的上下两侧)
|y2-y1|(A、B在x轴的上下两侧)
又△ABF2的面积═1 /2 ×|r(|AB|+|BF2|+|F2A|="1" /2 ×(2a+2a)=2a=8.
所以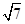 |y2-y1|=8,|y2-y1|=
|y2-y1|=8,|y2-y1|=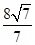 .故答案为
.故答案为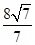
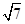 7 ,
7 ,左、右焦点F1(-
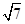 ,0)、F2(
,0)、F2( 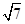 ,0),
,0),△ABF2的内切圆面积为π,则内切圆的半径为r=1,
而△ABF2的面积=△AF1F2的面积+△BF1F2的面积="1" /2 ×|y1|×|F1F2|+1/ 2 ×|y2|×|F1F2|="1" /2 ×(|y1|+|y2|)×|F1F2|=
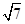 |y2-y1|(A、B在x轴的上下两侧)
|y2-y1|(A、B在x轴的上下两侧)又△ABF2的面积═1 /2 ×|r(|AB|+|BF2|+|F2A|="1" /2 ×(2a+2a)=2a=8.
所以
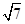 |y2-y1|=8,|y2-y1|=
|y2-y1|=8,|y2-y1|=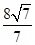 .故答案为
.故答案为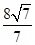

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 ,
, 是平面上一动点,且满足
是平面上一动点,且满足 ,
, 对应的方程;
对应的方程; 在曲线
在曲线 作曲线
作曲线 ,且
,且 满足
满足 ,试判断动直线
,试判断动直线 是否过定点,并证明你的结论.
是否过定点,并证明你的结论.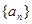 ,
, 中,
中,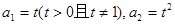 ,且
,且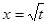 是函数
是函数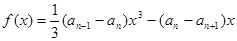 的一个极值点.
的一个极值点.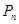 的坐标为(1,
的坐标为(1,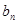 )(
)(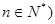 ,过函数
,过函数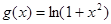 图像上的点
图像上的点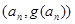 的切线始终与
的切线始终与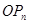 平行(O 为原点),求证:当
平行(O 为原点),求证:当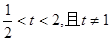 时,不等式
时,不等式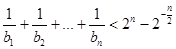 对任意
对任意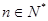 都成立.
都成立. 是单位圆
是单位圆 上的任意一点,
上的任意一点, 是过点
是过点 轴垂直的直线,
轴垂直的直线, 是直线
是直线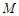 在直线
在直线 . 当点
. 当点 .
. 的直线交曲线
的直线交曲线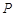 ,
,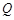 两点,其中
两点,其中 轴上的射影为点
轴上的射影为点 ,直线
,直线 交曲线
交曲线 . 是否存在
. 是否存在 ,使得对任意的
,使得对任意的 ,都有
,都有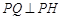 ?若存在,求
?若存在,求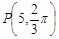 ,
, 为极点,求使
为极点,求使 是正三角形的
是正三角形的 点的极坐标为_______ __
点的极坐标为_______ __
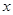 轴的非负半轴为极轴建立极坐标系,曲线E的极坐标方程为
轴的非负半轴为极轴建立极坐标系,曲线E的极坐标方程为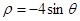 ,曲线F的参数方程为
,曲线F的参数方程为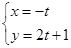 (t为参数)
(t为参数)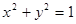 上运动时,它与定点Q(3,0)所连线段PQ的中点M的轨迹方程是:
上运动时,它与定点Q(3,0)所连线段PQ的中点M的轨迹方程是: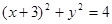
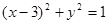
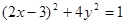
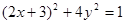
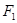 、
、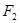 是椭圆
是椭圆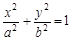
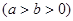 的左、右焦点,
的左、右焦点,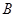 是该椭圆短轴的一个端点,直线
是该椭圆短轴的一个端点,直线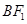 与椭圆
与椭圆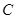 交于点
交于点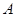 ,若
,若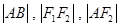 成等差数列,则该椭圆的离心率为 .
成等差数列,则该椭圆的离心率为 .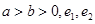 分别是圆锥曲线
分别是圆锥曲线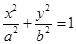 和
和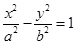 的离心率,设
的离心率,设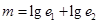 ,则
,则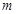 的取值范围是 .
的取值范围是 .