题目内容
为了加快经济的发展,某省选择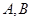 两城市作为龙头带动周边城市的发展,决定在
两城市作为龙头带动周边城市的发展,决定在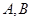 两城市的周边修建城际轻轨,假设
两城市的周边修建城际轻轨,假设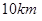 为一个单位距离,
为一个单位距离, 两城市相距
两城市相距 个单位距离,设城际轻轨所在的曲线为
个单位距离,设城际轻轨所在的曲线为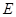 ,使轻轨
,使轻轨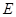 上的点到
上的点到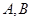 两城市的距离之和为
两城市的距离之和为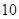 个单位距离,
个单位距离,
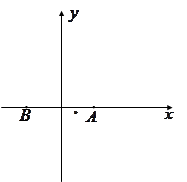
(1)建立如图的直角坐标系,求城际轻轨所在曲线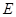 的方程;
的方程;
(2)若要在曲线 上建一个加油站
上建一个加油站 与一个收费站
与一个收费站 ,使
,使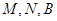 三点在一条直线上,并且
三点在一条直线上,并且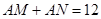 个单位距离,求
个单位距离,求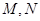 之间的距离有多少个单位距离?
之间的距离有多少个单位距离?
(3)在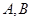 两城市之间有一条与
两城市之间有一条与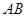 所在直线成
所在直线成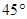 的笔直公路
的笔直公路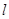 ,直线
,直线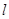 与曲线
与曲线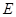 交于
交于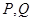 两点,求四边形
两点,求四边形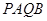 的面积的最大值.
的面积的最大值.
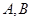 两城市作为龙头带动周边城市的发展,决定在
两城市作为龙头带动周边城市的发展,决定在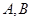 两城市的周边修建城际轻轨,假设
两城市的周边修建城际轻轨,假设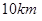 为一个单位距离,
为一个单位距离,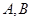 两城市相距
两城市相距 个单位距离,设城际轻轨所在的曲线为
个单位距离,设城际轻轨所在的曲线为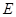 ,使轻轨
,使轻轨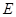 上的点到
上的点到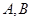 两城市的距离之和为
两城市的距离之和为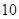 个单位距离,
个单位距离,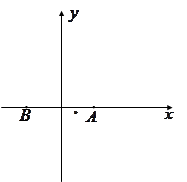
(1)建立如图的直角坐标系,求城际轻轨所在曲线
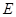 的方程;
的方程;(2)若要在曲线
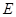 上建一个加油站
上建一个加油站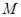 与一个收费站
与一个收费站 ,使
,使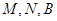 三点在一条直线上,并且
三点在一条直线上,并且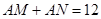 个单位距离,求
个单位距离,求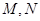 之间的距离有多少个单位距离?
之间的距离有多少个单位距离?(3)在
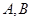 两城市之间有一条与
两城市之间有一条与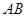 所在直线成
所在直线成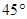 的笔直公路
的笔直公路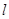 ,直线
,直线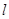 与曲线
与曲线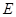 交于
交于 两点,求四边形
两点,求四边形 的面积的最大值.
的面积的最大值.(1) (2)8(3)
(2)8(3)
 (2)8(3)
(2)8(3)
(1)根据题目条件选取适当的坐标系,本小题应该以AB所在直线为x轴,AB的垂直平分线为y轴建立直角坐标系,这样得到的轨迹方程是标准方程,有利于下一步的计算.
(2)由椭圆的定义可知|AM|+|AN|+|BM|+|BN|=20,|AM|+|AN|=12,所以|MN|=8.
(3)先求出四边形 的面积的表达式,设直线方程为y=x+t,然后与椭圆方程联立,消x后得到关于y的一元二次方程,借助韦达定理,根据
的面积的表达式,设直线方程为y=x+t,然后与椭圆方程联立,消x后得到关于y的一元二次方程,借助韦达定理,根据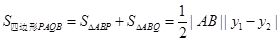 ,
,
求出面积关于t的函数表达式,利用函数的方法求最值即可.
解:(1)以AB为x轴,以AB中点为原点O建立直角坐标系,设曲线E上点 ,
,
∵|PA|+|PB|=10>|AB|=8
∴动点轨迹为椭圆,且a=5,c=4,从面b=3.
∴曲线E的方程为 4分
4分
(2)由|AM|+|AN|+|BM|+|BN|=20,|AM|+|AN|=12,所以|MN|=8 8分
(3)将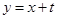 代入
代入 ,得
,得
设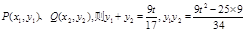
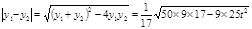

所以当t=0时,面积最大是 ,此时直线为l:y=x 13分
,此时直线为l:y=x 13分
(2)由椭圆的定义可知|AM|+|AN|+|BM|+|BN|=20,|AM|+|AN|=12,所以|MN|=8.
(3)先求出四边形
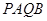 的面积的表达式,设直线方程为y=x+t,然后与椭圆方程联立,消x后得到关于y的一元二次方程,借助韦达定理,根据
的面积的表达式,设直线方程为y=x+t,然后与椭圆方程联立,消x后得到关于y的一元二次方程,借助韦达定理,根据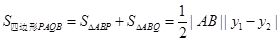 ,
,求出面积关于t的函数表达式,利用函数的方法求最值即可.
解:(1)以AB为x轴,以AB中点为原点O建立直角坐标系,设曲线E上点
 ,
,∵|PA|+|PB|=10>|AB|=8
∴动点轨迹为椭圆,且a=5,c=4,从面b=3.
∴曲线E的方程为
 4分
4分(2)由|AM|+|AN|+|BM|+|BN|=20,|AM|+|AN|=12,所以|MN|=8 8分
(3)将
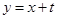 代入
代入 ,得
,得
设
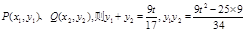
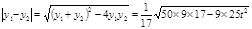

所以当t=0时,面积最大是
 ,此时直线为l:y=x 13分
,此时直线为l:y=x 13分
练习册系列答案
相关题目
 ,
, 是平面上一动点,且满足
是平面上一动点,且满足 ,
, 对应的方程;
对应的方程; 在曲线
在曲线 作曲线
作曲线 ,且
,且 满足
满足 ,试判断动直线
,试判断动直线 是否过定点,并证明你的结论.
是否过定点,并证明你的结论.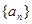 ,
, 中,
中,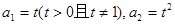 ,且
,且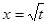 是函数
是函数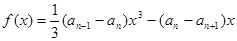 的一个极值点.
的一个极值点.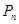 的坐标为(1,
的坐标为(1,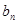 )(
)(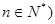 ,过函数
,过函数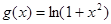 图像上的点
图像上的点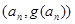 的切线始终与
的切线始终与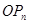 平行(O 为原点),求证:当
平行(O 为原点),求证:当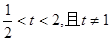 时,不等式
时,不等式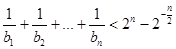 对任意
对任意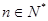 都成立.
都成立.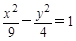 与直线
与直线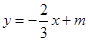 (
(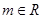 )的公共点的个数为( ).
)的公共点的个数为( ).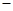 3,0),C(3,0)另两边所在直线的斜率之积为
3,0),C(3,0)另两边所在直线的斜率之积为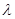 (
( 中,
中, ,一个圆心为M,半径为
,一个圆心为M,半径为 的圆在
的圆在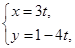 (
(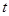 为参数)与圆
为参数)与圆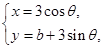 (
(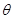 为参数)相切,则
为参数)相切,则 ( )
( )
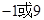
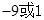
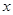 轴的非负半轴为极轴建立极坐标系,曲线E的极坐标方程为
轴的非负半轴为极轴建立极坐标系,曲线E的极坐标方程为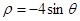 ,曲线F的参数方程为
,曲线F的参数方程为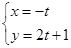 (t为参数)
(t为参数)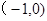 的抛物线的标准方程为( )
的抛物线的标准方程为( )