Question

【题目】如图1，在边长为2的等边△ABC中，D，E分别为边AC，AB的中点．将△ADE沿DE折起，使得AB⊥AD，得到如图2的四棱锥A﹣BCDE，连结BD，CE，且BD与CE交于点H．

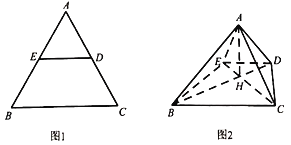
（1）证明：；

（2）设点B到平面AED的距离为h1，点E到平面ABD的距离为h2，求的值．

Answer 1

【答案】（1）证明见解析；（2）．

【解析】

（1）在图1中，证明BD⊥AC，ED∥BC，则在图2中，有，得DH，然后证明△BAD∽△AHD，可得∠AHD＝∠BAD＝90°，即AH⊥BD；

（2）由VB﹣AED＝VE﹣ABD，得，分别求出三角形ABD与三角形AED的面积得答案．

（1）证明：在图1中，∵△ABC为等边三角形，且D为边AC的中点，∴BD⊥AC，

在△BCD中，BD⊥CD，BC＝2，CD＝1，∴BD，

∵D、E分别为边AC、AB的中点，∴ED∥BC，

在图2中，有，∴DH．

在Rt△BAD中，BD，AD＝1，

在△BAD和△AHD中，∵，∠BDA＝∠ADH

∴△BAD∽△AHD．

∴∠AHD＝∠BAD＝90°，即AH⊥BD；

（2）解：∵VB﹣AED＝VE﹣ABD，

∴，则．

∵△AED是边长为1的等边三角形，∴．

在Rt△ABD中，BD，AD＝1，则AB．

∴，

则．