题目内容
8.已知数列{an}中,a1=a(实数a为常数),a2=2,Sn是其前n项和,且Sn=$\frac{n({a}_{n}-{a}_{1})}{2}$.数列{bn}是等比数列,b1=2,a4恰为S4与b2-1的等比中项.(Ⅰ)证明:数列{an}是等差数列;
(Ⅱ)求数列{bn}的通项公式;
(Ⅲ)若c1=$\frac{3}{2}$,当n≥2时cn=$\frac{1}{{b}_{n-1}+1}$+$\frac{1}{{b}_{n-1}+2}$+…+$\frac{1}{{b}_{n}}$,{cn}的前n项和为Tn,求证:对任意n≥2,都有12Tn≥6n+13.
分析 (Ⅰ)当n=1可得a1=a=0,进而有Sn=$\frac{n{a}_{n}}{2}$,当n≥2时利用累乘法可得an=$\frac{{a}_{n}}{{a}_{n-1}}$•$\frac{{a}_{n-1}}{{a}_{n-2}}$•…•$\frac{{a}_{3}}{{a}_{2}}$•a2=2(n-1),即得结论;
(Ⅱ)设等比数列{bn}的公比为q,则bn=2qn-1,利用a4恰为S4与b2-1的等比中项可得公比q=2,进而可得结论;
(Ⅲ)利用放缩法可得cn>$\frac{1}{2}$,进而有Tn>$\frac{6n+13}{12}$,即得结论.
解答 (Ⅰ)证明:令n=1可得a1=S1=0,即a=0.所以Sn=$\frac{n{a}_{n}}{2}$.
当n≥2时an=Sn-Sn-1=$\frac{n{a}_{n}}{2}$-$\frac{(n-1){a}_{n-1}}{2}$,可得(n-2)an=(n-1)an-1,
当n≥3时$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{n-1}{n-2}$,所以an=$\frac{{a}_{n}}{{a}_{n-1}}$•$\frac{{a}_{n-1}}{{a}_{n-2}}$•…•$\frac{{a}_{3}}{{a}_{2}}$•a2=2(n-1).
显然当n=1、2时,满足上式.所以an=2(n-1),n∈N*.
∴an+1-an=2,所以数列{an}是等差数列,其通项公式是an=2(n-1),n∈N*.
(Ⅱ)解:设等比数列{bn}的公比为q,所以bn=b1qn-1=2qn-1,
∵a4恰为S4与b2-1的等比中项,
∴a4=6,S4=12,b2=2q,
所以62=12×(2q-1),解得q=2,
所以bn=2n,n∈N*.
(Ⅲ)证明:n≥2时,Tn=c1+c2+…+cn
=(1+$\frac{1}{2}$)+($\frac{1}{{2}^{1}+1}$+$\frac{1}{{2}^{2}}$)+($\frac{1}{{2}^{2}+1}$+$\frac{1}{{2}^{2}+2}$+$\frac{1}{{2}^{2}+3}$+$\frac{1}{{2}^{3}}$)+…+($\frac{1}{{2}^{n-1}+1}$+$\frac{1}{{2}^{n-1}+2}$+…+$\frac{1}{{2}^{n}}$),
而n≥2时,cn=$\frac{1}{{2}^{n-1}+1}$+$\frac{1}{{2}^{n-1}+2}$+…+$\frac{1}{{2}^{n}}$>$\frac{1}{{2}^{n}}$+$\frac{1}{{2}^{n}}$+…+$\frac{1}{{2}^{n}}$=$\frac{{2}^{n}-({2}^{n-1}-1)+1}{{2}^{n}}$=$\frac{{2}^{n-1}}{{2}^{n}}$=$\frac{1}{2}$,
所以当n=2时T2=1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$=$\frac{25}{12}$=$\frac{6×2+13}{12}$.
当n≥3时Tn=c1+c2+…+cn
>1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{2}$+$\frac{1}{2}$+$\frac{1}{2}$+…+$\frac{1}{2}$=$\frac{6n+13}{12}$,
∴对任意n≥2,都有12Tn≥6n+13.
点评 本题考查求数列的通项,判断数列为等差数列,以及前n项和的大小范围,注意解题方法的积累,属于中档题.

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案| A. | 24 | B. | 12 | C. | 6 | D. | 4 |
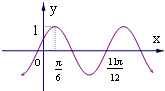 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象,如图所示,则将y=f(x)的图象向右平移$\frac{π}{3}$个单位后,得到的图象解析式为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象,如图所示,则将y=f(x)的图象向右平移$\frac{π}{3}$个单位后,得到的图象解析式为( )| A. | y=sin(2x-$\frac{π}{6}$) | B. | y=cos2x | C. | y=sin(2x+$\frac{5π}{6}$) | D. | y=-cos2x |
| A. | $\frac{1}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{30}}{10}$ |
 如图,在五面体ABCDEF中,AB∥CD∥EF,CD=EF=CF=2AB=2AD=2,∠DCF=60°,AD⊥CD,平面CDEF⊥平面ABCD.
如图,在五面体ABCDEF中,AB∥CD∥EF,CD=EF=CF=2AB=2AD=2,∠DCF=60°,AD⊥CD,平面CDEF⊥平面ABCD. 已知PA⊥平面ABCD,CD⊥AD,BA⊥AD,CD=AD=AP=4,AB=2.
已知PA⊥平面ABCD,CD⊥AD,BA⊥AD,CD=AD=AP=4,AB=2.