题目内容
17．若函数y=lg（x2+ax+a+$\frac{5}{4}$）的定义域为R，则a的取值范围为（-1，5）．分析 由题意可得x2+ax+a+$\frac{5}{4}$＞0恒成立，则△＜0，解二次不等式即可得到a的范围．
解答 解：函数y=lg（x2+ax+a+$\frac{5}{4}$）的定义域为R，
即有x2+ax+a+$\frac{5}{4}$＞0恒成立，
则△＜0，
即为a2-4（a+$\frac{5}{4}$）＜0，
解得-1＜a＜5，
则a的范围是（-1，5）．
故答案为：（-1，5）．
点评 本题考查函数的定义域的运用：求参数的范围，主要考查对数函数的定义域和运用，考查二次不等式的解法，属于中档题．
练习册系列答案
相关题目
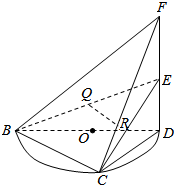如图：$\widehat{BCD}$是直径为$2\sqrt{2}$的半圆，O为圆心，C是$\widehat{BD}$上一点，且$\widehat{BC}=2\widehat{CD}$．DF⊥CD，且DF=2，$BF=2\sqrt{3}$，E为FD的中点，Q为BE的中点，R为FC上一点，且FR=3RC．
2．把函数f（x）=sin（2x+ϕ）$（|ϕ|＜\frac{π}{2}）$的图象向左平移$\frac{π}{6}$个单位，得到函数g（x）的图象，若g（x）的图象关于$（-\frac{π}{3}，0）$对称，则$f（-\frac{π}{2}）$=（ ）
| A． | $-\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | $-\frac{{\sqrt{3}}}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
如图，某几何体的正视图、侧视图、俯视图均为面积为2的等腰直角三角形，则该多面体面的个数为4，体积为$\frac{4}{3}$．