Question

7．直三棱锥ABC-A₁B₁C₁中，∠BCA=90°，M，N分别是A₁B₁，A₁C₁的中点，BC=CA=CC₁，则BM与AN所成角的余弦值为（　　）

• A． $\frac{1}{10}$
• B． $\frac{2}{5}$
• C． $\frac{\sqrt{2}}{2}$
• D． $\frac{\sqrt{30}}{10}$

Answer 1

分析 画出图形，建立空间直角坐标系，从而求出向量$\overrightarrow{BM}$，$\overrightarrow{AN}$的坐标，从而BM与AN所成角的余弦值为|$＜\overrightarrow{BM}，\overrightarrow{AN}＞$|=$\frac{|\overrightarrow{BM}•\overrightarrow{AN}|}{|\overrightarrow{BM}||\overrightarrow{AN}|}$．

解答 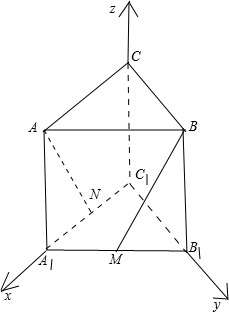解：根据已知条件，分别以C₁A₁，C₁B₁，C₁C所在直线为x，y，z轴，建立如图所示空间直角坐标系，设CA=2，则：
A（2，0，2），N（1，0，0），B（0，2，2），A₁（2，0，0），B₁（0，2，0），M（1，1，0）；
∴$\overrightarrow{BM}=（1，-1，-2），\overrightarrow{AN}=（-1，0，-2）$；
∴$cos＜\overrightarrow{BM}，\overrightarrow{AN}＞=\frac{3}{\sqrt{6}•\sqrt{5}}=\frac{\sqrt{30}}{10}$；
∴BM与AN所成角的余弦值为$\frac{\sqrt{30}}{10}$．
故选：D．

点评 考查通过建立空间直角坐标系，利用空间向量求异面直线所成角的方法，能求出空间点的坐标，向量夹角余弦的坐标公式，弄清向量夹角和异面直线所成角的关系．