题目内容
(本小题满分12分)设数列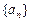 、
、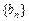 、
、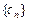 满足:
满足: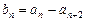 ,
,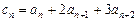 (n=1,2,3,…), 证明:
(n=1,2,3,…), 证明: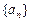 为等差数列的充分必要条件是
为等差数列的充分必要条件是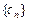 为等差数列且
为等差数列且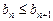 (n=1,2,3,…)
(n=1,2,3,…)
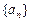 、
、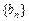 、
、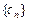 满足:
满足: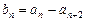 ,
,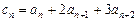 (n=1,2,3,…), 证明:
(n=1,2,3,…), 证明: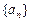 为等差数列的充分必要条件是
为等差数列的充分必要条件是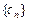 为等差数列且
为等差数列且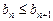 (n=1,2,3,…)
(n=1,2,3,…)见解析
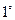 必要性:设数列
必要性:设数列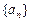 是公差为
是公差为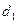 的等差数列,则:
的等差数列,则: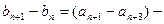
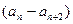 =
=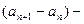
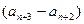 =
=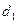 -
-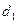 =0,
=0,∴
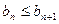 (n=1,2,3,…)成立;
(n=1,2,3,…)成立;又
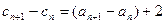
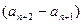
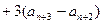 =6
=6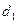 (常数)(n=1,2,3,…)
(常数)(n=1,2,3,…)∴数列
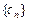 为等差数列.
为等差数列.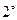 充分性:设数列
充分性:设数列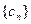 是公差为
是公差为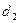 的等差数列,且
的等差数列,且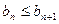 (n=1,2,3,…),
(n=1,2,3,…),∵
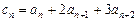 ……① ∴
……① ∴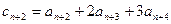 ……②
……②①-②得:
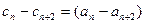
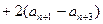
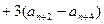 =
=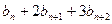
∵
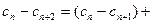
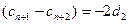
∴
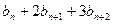
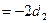 ……③ 从而有
……③ 从而有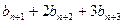
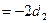 ……④
……④④-③得:
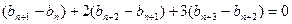 ……⑤
……⑤∵
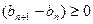 ,
,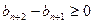 ,
,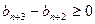 ,
,∴由⑤得:
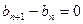 (n=1,2,3,…),
(n=1,2,3,…),由此,不妨设
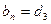 (n=1,2,3,…),则
(n=1,2,3,…),则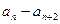
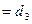 (常数)
(常数)故
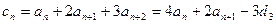 ……⑥
……⑥从而
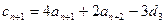
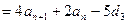 ……⑦
……⑦⑦-⑥得:
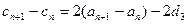 ,
,故
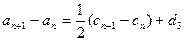
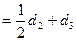 (常数)(n=1,2,3,…),
(常数)(n=1,2,3,…),∴数列
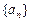 为等差数列.
为等差数列.综上所述:
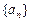 为等差数列的充分必要条件是
为等差数列的充分必要条件是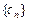 为等差数列且
为等差数列且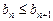 (n=1,2,3,…).
(n=1,2,3,…).
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
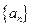 的前
的前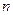 项和为
项和为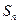 ,已知对任意正整数
,已知对任意正整数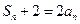 成立。
成立。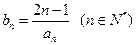 ,数列
,数列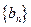 的前
的前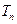 ,求证:
,求证: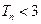 。
。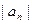 满足:
满足: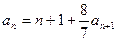 ,且存在大于1的整数k使
,且存在大于1的整数k使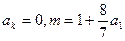 。
。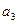 表示m(不必化简)
表示m(不必化简)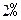 并按复利计算,问每年应该存入多少钱?
并按复利计算,问每年应该存入多少钱?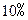 的速度增长,这个城市近10 年的国内生产总值一共是多少?
的速度增长,这个城市近10 年的国内生产总值一共是多少?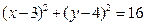 ,直线
,直线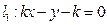 .
.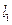 与圆交于两个不同点
与圆交于两个不同点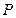 、
、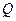 ,求实数
,求实数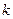 的取值范围;
的取值范围;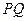 的中点为
的中点为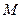 ,
,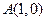 ,且
,且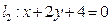 的交点为
的交点为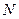 ,求证:
,求证: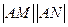 为定值
为定值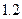 元/km,起步价为10元,即最初的4km(不含4千米)计费10元.如果某人乘坐该市的出租车去往14 km处的目的地,且一路畅通,等候时间为0,需要支付多少车费?
元/km,起步价为10元,即最初的4km(不含4千米)计费10元.如果某人乘坐该市的出租车去往14 km处的目的地,且一路畅通,等候时间为0,需要支付多少车费?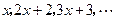 为等比数列,求这个数列的第
为等比数列,求这个数列的第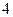 项.
项.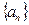 中,
中,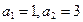 ,且
,且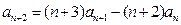 ,(n∈N*),求通项公式
,(n∈N*),求通项公式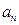 .
.