题目内容
已知数列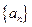 满足,
满足,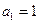 ,
,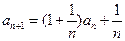 (n∈N*)。
(n∈N*)。
(I)设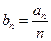 ,求数列
,求数列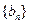 的通项公式;
的通项公式;
(II)若对任意给定的正整数m,使得不等式an+t≥2m(n∈N*)成立的所有n中的最小值为m+2,求实数t的取值范围。
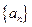 满足,
满足,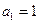 ,
,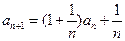 (n∈N*)。
(n∈N*)。(I)设
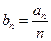 ,求数列
,求数列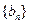 的通项公式;
的通项公式;(II)若对任意给定的正整数m,使得不等式an+t≥2m(n∈N*)成立的所有n中的最小值为m+2,求实数t的取值范围。
(I)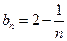
(II)[-3,-1)
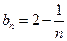
(II)[-3,-1)
因为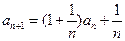 ,则
,则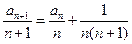 ,即
,即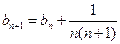 , (2分)
, (2分)
所以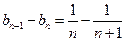 。又
。又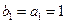 ,所以
,所以
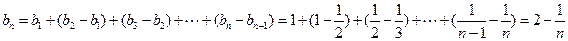 。
。
故数列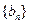 的通项公式是
的通项公式是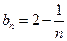 。 (6分)
。 (6分)
(II)因为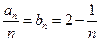 ,则
,则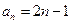 。 (7分)
。 (7分)
由an+t≥2m,得2n-1+t≥2m,即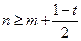 。 (8分)
。 (8分)
据题意,区间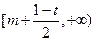 内的最小正整数为m+2,则
内的最小正整数为m+2,则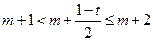 ,(10分)
,(10分)
即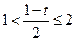 ,所以-3≤t<-1。
,所以-3≤t<-1。
故实数t的取值范围是[-3,-1)。 (12分)
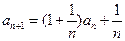 ,则
,则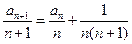 ,即
,即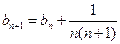 , (2分)
, (2分)所以
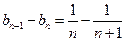 。又
。又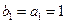 ,所以
,所以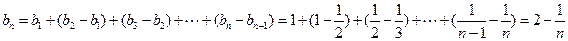 。
。故数列
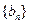 的通项公式是
的通项公式是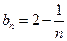 。 (6分)
。 (6分)(II)因为
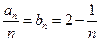 ,则
,则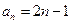 。 (7分)
。 (7分)由an+t≥2m,得2n-1+t≥2m,即
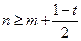 。 (8分)
。 (8分)据题意,区间
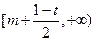 内的最小正整数为m+2,则
内的最小正整数为m+2,则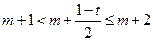 ,(10分)
,(10分)即
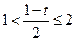 ,所以-3≤t<-1。
,所以-3≤t<-1。故实数t的取值范围是[-3,-1)。 (12分)

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 时,求Sn.
时,求Sn.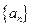 的前
的前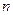 项和为
项和为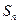 ,已知对任意正整数
,已知对任意正整数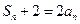 成立。
成立。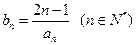 ,数列
,数列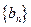 的前
的前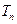 ,求证:
,求证: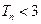 。
。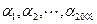 为2008个整数,且
为2008个整数,且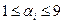 (
(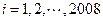 )。如果存在某个
)。如果存在某个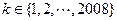 ,使得2008位数
,使得2008位数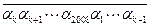 被101整除,试证明:对一切
被101整除,试证明:对一切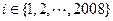 ,2008位数
,2008位数 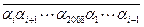 均能被101整除。
均能被101整除。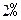 并按复利计算,问每年应该存入多少钱?
并按复利计算,问每年应该存入多少钱?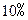 的速度增长,这个城市近10 年的国内生产总值一共是多少?
的速度增长,这个城市近10 年的国内生产总值一共是多少?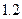 元/km,起步价为10元,即最初的4km(不含4千米)计费10元.如果某人乘坐该市的出租车去往14 km处的目的地,且一路畅通,等候时间为0,需要支付多少车费?
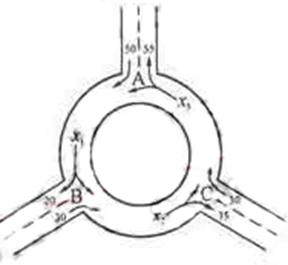
元/km,起步价为10元,即最初的4km(不含4千米)计费10元.如果某人乘坐该市的出租车去往14 km处的目的地,且一路畅通,等候时间为0,需要支付多少车费?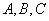 的机动车辆数如图所示(20,30;35,30;55,50),图中
的机动车辆数如图所示(20,30;35,30;55,50),图中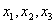 分别表示该时段单位时间通过路段
分别表示该时段单位时间通过路段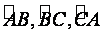 的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则( )
的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则( )