题目内容
【题目】如图,平面ABCD⊥平面ADEF,四边形ABCD为菱形,四边形ADEF为矩形,M、N分别是EF、BC的中点,AB=2AF=2,∠CBA=60°.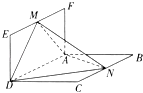
(1)求证:AN⊥DM;
(2)求直线MN与平面ADEF所成的角的正切值;
(3)求三棱锥D﹣MAN的体积.
【答案】
(1)证明:连接AC,在菱形ABCD中,
∵∠CBA=60°且AB=BC,∴△ABC为等边三角形.
∵N为BC的中点,∴AN⊥BC,
又∵BC∥AD,∴AN⊥AD,
∵平面ABCD⊥平面ADEF,AN平面ADEF,平面ABCD∩平面ADEF=AD
∴AN⊥平面ADEF,
∵DM平面ADEF,
∴AN⊥DM;
(2)解:由(1)知,NA⊥平面ADEF,
∴∠NMA为直线MN与平面ADEF所成的角,
∵四边形ADEF为矩形,AD=2AF=2,M是EF的中点,
∴AF=FM=1,
∴△AMF为等腰直角三角形,
∴AM= ![]() ,
,
∵△ABC为边长为2的等边三角形且N是BC的中点,
∴AN= ![]() ,
,
在Rt△NAM中,tan∠NMA= ![]() =
= ![]()
(3)解:∵四边形ADEF为矩形,M是EF的中点,AB=2AF=2,
∴ME=DE=1,且DM=AM= ![]() ,
,
∴AD2=AM2+DM2,
∴∠AMD=90°,
∴S△AMD= ![]() =1.
=1.
由(1)NA⊥平面ADEF,
∴三棱锥D﹣MAN的体积=三棱锥N﹣MAD的体积= ![]() =
= ![]() .
.

【解析】(1)连接AC,证明AN⊥AD,利用平面与平面垂直的性质证明AN⊥平面ADEF,即可证明AN⊥DM;(2)由(1)知,NA⊥平面ADEF,可得∠NMA为直线MN与平面ADEF所成的角,求出AN,AM,即可求直线MN与平面ADEF所成的角的正切值;(3)利用三棱锥D﹣MAN的体积=三棱锥N﹣MAD的体积,即可求三棱锥D﹣MAN的体积.
【考点精析】利用空间角的异面直线所成的角对题目进行判断即可得到答案,需要熟知已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 .
.

【题目】甲、乙两位学生参加数学竞赛培训,在培训期间,他们参加的5次预赛成绩记录如下:
甲 | 82 | 82 | 79 | 95 | 87 |
乙 | 95 | 75 | 80 | 90 | 85 |
(1)请用茎叶图表示这两组数据;
(2)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(3)现要从中选派一人参加9月份的全国数学联赛,从统计学的角度考虑,你认为选派哪位学生参加合适?请说明理由.