题目内容
(15分)点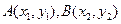 是抛物线
是抛物线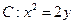 上的不同两点,过
上的不同两点,过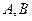 分别作抛物线
分别作抛物线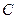 的切线,两条切线交于点
的切线,两条切线交于点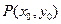 。
。
(1)求证: 是
是 与
与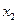 的等差中项;
的等差中项;
(2)若直线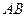 过定点
过定点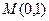 ,求证:原点
,求证:原点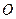 是
是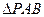 的垂心;
的垂心;
(3)在(2)的条件下,求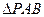 的重心
的重心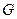 的轨迹方程。
的轨迹方程。
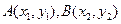 是抛物线
是抛物线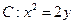 上的不同两点,过
上的不同两点,过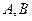 分别作抛物线
分别作抛物线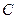 的切线,两条切线交于点
的切线,两条切线交于点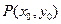 。
。(1)求证:
 是
是 与
与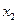 的等差中项;
的等差中项;(2)若直线
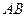 过定点
过定点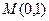 ,求证:原点
,求证:原点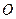 是
是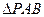 的垂心;
的垂心;(3)在(2)的条件下,求
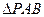 的重心
的重心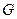 的轨迹方程。
的轨迹方程。(1)证明见解析。
(2)证明见解析。
(3)
(2)证明见解析。
(3)

(1)对 求导 得
求导 得 ,
,
所以直线 ,即
,即
同理, 直线 ,解得
,解得
所以 是
是 与
与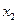 的等差中项; (5分)
的等差中项; (5分)
(2)设直线 ,代入
,代入 整理得
整理得 .
.
 ,得
,得
 即
即 ;
;
 ,
,
 ,
,
 , 同理
, 同理 ,
,
所以原点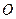 是
是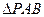 的垂心;(10分,只需证明
的垂心;(10分,只需证明 两个垂直就得满分)
两个垂直就得满分)
(3)设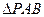 的重心
的重心 ,则
,则
 ,
,

因为 ,所以点
,所以点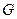 的轨迹方程为
的轨迹方程为 . (15分)
. (15分)
 求导 得
求导 得 ,
,所以直线
 ,即
,即
同理, 直线
 ,解得
,解得
所以
 是
是 与
与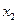 的等差中项; (5分)
的等差中项; (5分)(2)设直线
 ,代入
,代入 整理得
整理得 .
. ,得
,得
 即
即 ;
; ,
,
 ,
, , 同理
, 同理 ,
,所以原点
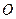 是
是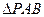 的垂心;(10分,只需证明
的垂心;(10分,只需证明 两个垂直就得满分)
两个垂直就得满分)(3)设
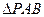 的重心
的重心 ,则
,则 ,
,
因为
 ,所以点
,所以点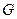 的轨迹方程为
的轨迹方程为 . (15分)
. (15分)
练习册系列答案
相关题目
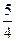 ,则A到顶点的距离等于________________.
,则A到顶点的距离等于________________.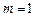 时,求椭圆的标准方程及其右准线的方程;
时,求椭圆的标准方程及其右准线的方程; 表示P点的坐标;
表示P点的坐标;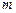 ,使得
,使得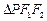 的边长是连续的自然数,若存在,求出这样的实数
的边长是连续的自然数,若存在,求出这样的实数 轴,抛物线上一点
轴,抛物线上一点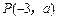 到焦点的距离为5,求抛物线的标准方程.
到焦点的距离为5,求抛物线的标准方程.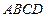 的两顶点
的两顶点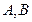 在抛物线
在抛物线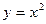 上,
上,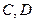 两点在直线
两点在直线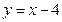 上,求正方形的边长
上,求正方形的边长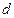 。
。 与点
与点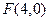 的距离比它到直线
的距离比它到直线 的距离大
的距离大 ,则点
,则点 ,焦点为
,焦点为 ,
, 是抛物线上的动点,则
是抛物线上的动点,则 的最大值为 .
的最大值为 .