题目内容
【题目】解答下列各题:
(1)已知扇形的周长为10cm,面积为4cm2,求扇形圆心角的弧度数.
(2)已知一扇形的圆心角是72°,半径等于20cm,求扇形的面积.
(3)已知一扇形的周长为40cm,求它的半径和圆心角取什么值时,才能使扇形的面积最大?最大面积是多少?
【答案】(1)![]() (2) 80π(3) 2, 最大值为100cm2
(2) 80π(3) 2, 最大值为100cm2
【解析】
(1)设扇形圆心角的弧度数为θ(0<θ<
2π),弧长为l,半径为r,
依题意有![]()
①代入②得r2-5r+4=0,解之得r1=1,r2=4.
当r=1时,l=8(cm),此时,θ=8rad>2πrad舍去.
当r=4时,l=2(cm),此时,θ=![]() =
=![]() rad.
rad.
(2)设扇形弧长为l,∵72°=72×![]() =
=![]() (rad),
(rad),
∴l=αR=![]() ×20=8π(cm).
×20=8π(cm).
∴S=![]() lR=
lR=![]() ×8π×20=80π(cm2).
×8π×20=80π(cm2).
(3)设扇形的圆心角为θ,半径为r,弧长为l,面积为S,则l+2r=40,
∴l=40-2r,∴S=![]() lr=
lr=![]() ×(40-2r)r=(20-r)r=-(r-10)2+100.
×(40-2r)r=(20-r)r=-(r-10)2+100.
∴当半径r=10cm时,扇形的面积最大.
这个最大值为100cm2,这时θ=![]() =
=![]() =2rad.
=2rad.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】已知某学校的特长班有50名学生,其中有体育生20名,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60),…,第五组[70,75],按上述分组方法得到的频率分布直方图如图所示.因为学习专业的原因,体育生常年进行系统的身体锻炼,艺术生则很少进行系统的身体锻炼,若前两组的学生中体育生有8名.
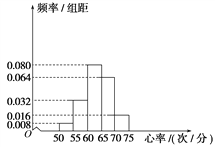
(1)根据频率分布直方图及题设数据完成下列2×2列联表.
心率小于60次/分 | 心率不小于60次/分 | 合计 | |
体育生 | 20 | ||
艺术生 | 30 | ||
合计50 |
(2)根据(1)中表格数据计算可知,________(填“有”或“没有”)99.5%的把握认为“心率小于60次/分与常年进行系统的身体锻炼有关”.
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】从集市上买回来的蔬菜仍存有残留农药,食用时需要清洗数次,统计表中的![]() 表示清洗的次数,
表示清洗的次数,![]() 表示清洗
表示清洗![]() 次后
次后![]() 千克该蔬菜残留的农药量(单位:微克).
千克该蔬菜残留的农药量(单位:微克).
|
|
|
|
|
|
|
|
|
|
|
|
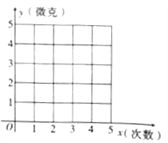
(1)在如图的坐标系中,描出散点图,并根据散点图判断,![]()
![]() 哪一个适宜作为清洗
哪一个适宜作为清洗![]() 次后
次后![]() 千克该蔬菜残留的农药量的回归方程类型;(给出判断即可,不必说明理由)
千克该蔬菜残留的农药量的回归方程类型;(给出判断即可,不必说明理由)
(2)根据判断及下面表格中的数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
表中![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3)对所求的回归方程进行残差分析.
附:①线性回归方程![]() 中系数计算公式分别为
中系数计算公式分别为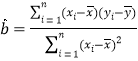 ,
,![]() ;
;
② ,
,![]() 说明模拟效果非常好;
说明模拟效果非常好;
③![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.


